RP2: Enthalpy Change

What is the main objective of this practical?

• To measure the enthalpy change (H∆) for a chemical reaction (like neutralisation) or a physical process (like dissolving a salt) using simple calorimetry.

What is the key apparatus used as a calorimeter in this experiment, and why?

• A polystyrene cup. It is a good insulator, which minimises heat loss to (or heat gain from) the surroundings, making the measured temperature change more accurate.

What is the purpose of placing a lid on the polystyrene cup?

• To further reduce heat loss to the surroundings, specifically by evaporation and convection.

What is the equation used to calculate the heat energy (q) absorbed or released?

q = mc∆T

• q = heat energy change (in Joules)

• m = mass of the solution being heated (in grams)

• c = specific heat capacity (in $J g^-1 K^-1)

• ∆T = the change in temperature (in K or °C)

What two key assumptions are made about the 'm' and 'c' values when using q = mc∆T

• Mass (m): The density of the (aqueous) solution is assumed to be the same as water (1.0 g cm^-3). Therefore, 50 cm³ of solution has a mass of 50 g.

• Heat Capacity (c): The specific heat capacity of the solution is assumed to be the same as pure water (4.18 J g^-1 K^-1).

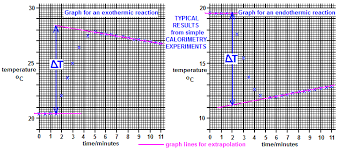
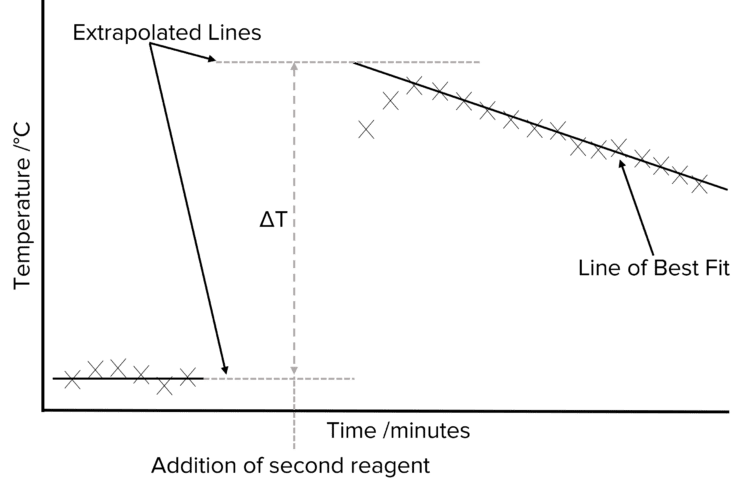
How is the maximum temperature change (∆T) found most accurately?

By plotting a graph of temperature vs. time.

• Plot the cooling section of the graph.

• Extrapolate the cooling curve (a line of best fit) back to the time of mixing (time = 0).

• ∆T is the difference between this extrapolated temperature and the initial temperature.

What is the equation used to convert the heat energy (q) into the molar enthalpy change (∆H)?

∆H = -q / moles

• q must be in kJ (divide J by 1000).

• moles is usually the moles of the limiting reactant, or moles of water formed in neutralisation.

• The negative sign corrects the sign: if the reaction is exothermic, ∆H is positive, 'q' is positive, but ∆H must be negative.

What is the main source of inaccuracy in this experiment?

• Heat loss to the surroundings (and to the apparatus, e.g., the thermometer).

  This makes the measured ∆T smaller than the true value, making the calculated enthalpy change less exothermic (or less endothermic).

⚠ SAFETY What is the main safety hazard when using acids (like HCl) and alkalis (like NaOH)?

• They are corrosive (or irritant at low concentrations). They can cause severe damage to skin and eyes.

⚠ SAFETY What is the main safety hazard associated with solid sodium hydroxide?

• It is corrosive and can cause severe burns. It is also hygroscopic (absorbs moisture) and the dissolving process is highly exothermic.

⚠ SAFETY What are the two essential safety precautions that must be taken during this practical?

• Wear eye protection (goggles) at all times to protect against splashes of corrosive chemicals.

• Wear a lab coat to protect skin and clothing. (Also: clear up spills immediately, and if chemicals make contact with skin, wash with copious amounts of water).

Question 1 (1 mark) State the main reason why a polystyrene cup is a suitable container for this experiment.

Answer: It is a good insulator / it minimises heat loss. (1)

Question 2 (2 marks) In an experiment to measure the enthalpy of neutralisation, 25.0 cm³ of acid was added to 25.0 cm³ of alkali. When calculating the heat energy change (q), state the two assumptions made about the solution.

• The density of the solution is the same as water (1.0 g cm^-3). (1)

• The specific heat capacity of the solution is the same as water (4.18 $J g^-1 K^-1). (1)

Question 5 (6 marks) Describe a method to find the enthalpy of neutralisation between 1.0 mol dm^-3 ethanoic acid and 1.0 mol dm^-3 sodium hydroxide, explaining how you would obtain an accurate value for the temperature change.

1. Rinse and fill a burette with 1.0 $mol dm^-3 ethanoic acid. Rinse a pipette with 1.0 $mol dm^-3 NaOH.

2. Use the pipette to add an accurate volume (e.g., 25.0 cm³) of the NaOH into a polystyrene cup.

3. Place the cup in a beaker (for stability) and place a lid on top. Use a thermometer (reading to ± 0.1 °C) inserted through a hole in the lid.

4. Measure the temperature of the NaOH solution every minute for 3 minutes to get a stable initial temperature.

5. At the 4th minute, add 25.0 cm³ of the ethanoic acid from the burette to the cup. Do not record the temperature at this time.

6. Continue recording the temperature of the mixture every minute from 5 minutes to 10 minutes, stirring gently.

7. To find ∆T: Plot a graph of temperature (y-axis) vs. time (x-axis). Extrapolate the cooling curve (the sloping line after the peak) back to 4 minutes. Read the temperature ($T_{max}$).

8. ∆T  = $T_max - T_initial.

9. Calculate q using q = mc∆T (where m = 50.0 g) and ∆H using ∆H = -q /moles (where moles = 0.025 mol).