AP Statistics

How do you check if there is outliers?

calculate IQR; anything above Q3+1.5(IQR) or below Q1-1.5(IQR) is an outlier

If a graph is skewed, should we calculate the median or the mean? Why?

median; it is resistant to skews and outliers

If a graph is roughly symmetrical, should we calculate the median or the mean? Why?

mean; generally is more accurate if the data has no outliers

What is in the five number summary?

Minimum, Q1, Median, Q3, Maximum

Relationship between variance and standard deviation?

variance=(standard deviation)^2

variance definition

the variance is roughly the average of the squared differences between each observation and the mean

standard deviation

the standard deviation is the square root of the variance

What should we use to measure spread if the median was calculated?

IQR

What should we use to measure spread if the mean was calculated?

standard deviation

What is the IQR? How much of the data does it represent?

Q3-Q1; 50%

How do you calculate standard deviation?

1. Type data into L1

2. Find mean with 1 Variable Stats

3. Turn L2 into (L1-mean)

4. Turn L3 into (L2)^2

5. Go to 2nd STAT over to MATH, select sum(

6. Type in L3

7. multiply it by (1/n-1)

8. Square root it

What is the formula for standard deviation?

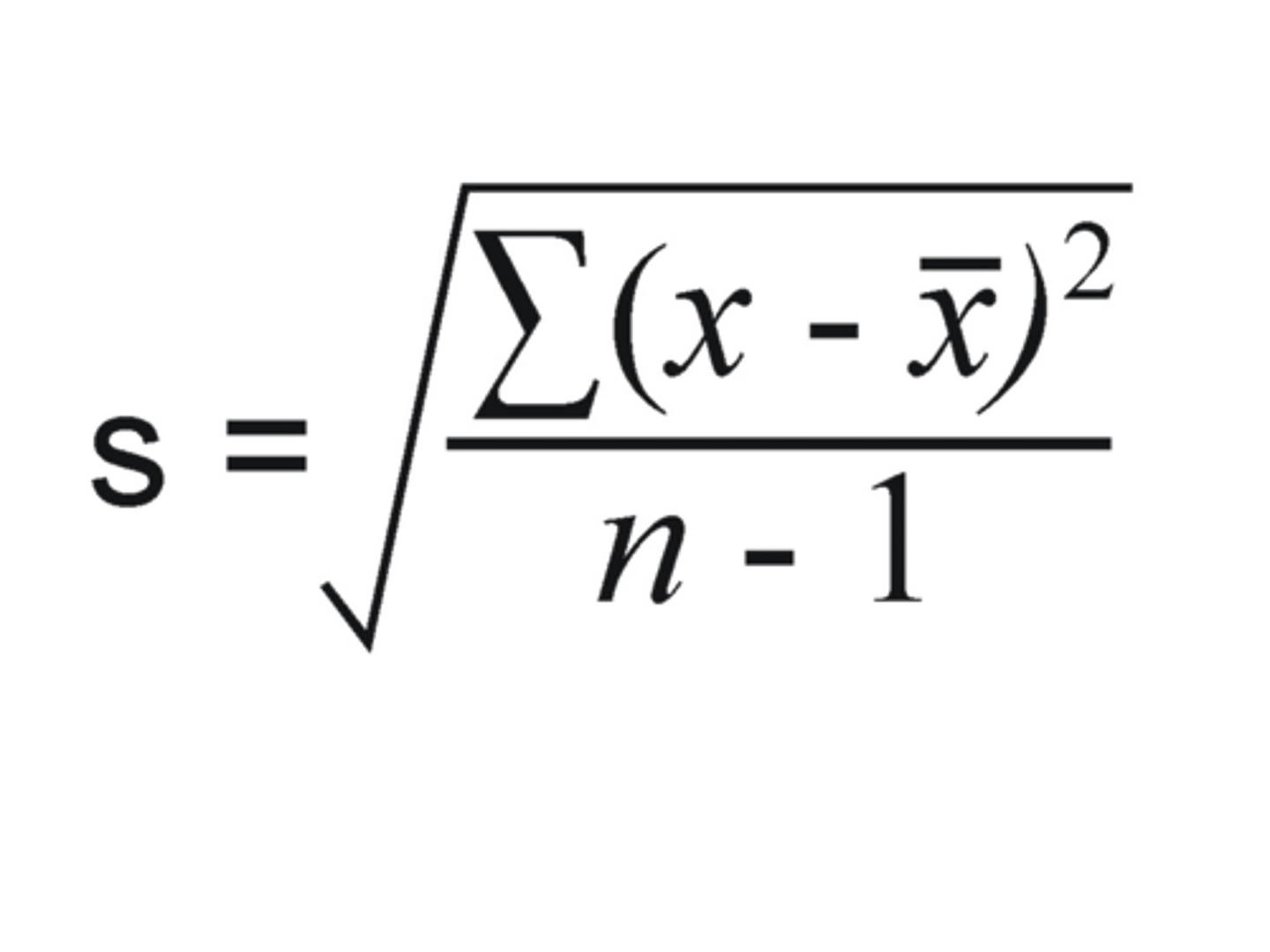
Categorical variables vs. Quantitative Variables

Categorical: individuals can be assigned to one of several groups or categories

Quantitative: takes numberical values

If a possible outlier is on the fence, is it an outlier?

No

Things to include when describing a distribution

Center (Mean or Median), Unusual Gaps or Outliers, Spread (Standard Deviation or IQR), Shape (Roughly Symmetric, slightly/heavily skewed left or right, bimodal, range)

Explain how to standardize a variable. What is the purpose of standardizing a variable?

Subtract the distribution mean and then divide by standard deviation. Tells us how many standard deviations from the mean an observation falls, and in what direction.

What effect does standardizing the values have on the distribution?

shape would be the same as the original distribution, the mean would become 0, the standard deviation would become 1

What is a density curve?

a curve that (a) is on or above the horizontal axis, and (b) has exactly an area of 1

Inverse Norm

when you want to find the percentile: invNorm (area, mean, standard deviation)

z

(x-mean)/standard deviation

pth percentile

the value with p percent observations less than is

cumulative relative frequency graph

can be used to describe the position of an individual within a distribution or to locate a specified percentile of the distribution

How to find and interpret the correlation coefficient r for a scatterplot

STAT plot, scatter, L1 and L2 (Plot 1: ON); STAT --> CALC --> 8:LinReg(a+bx)

No r? --> 2nd 0 (Catalog) down to Diagnostic ON

r

tells us the strength of a LINEAR association. -1 to 1. Not resistant to outliers

r^2

the proportion (percent) of the variation in the values of y that can be accounted for by the least squares regression line

residual plot

a scatterplot of the residuals against the explanatory variable. Residual plots help us assess how well a regression line fits the data. It should have NO PATTERN

regression line

a line that describes how a response variable y changes as an explanatory variable x changes. We often use a regression line to predict the value of y for a given value of x.

residual formula

residual=y-y(hat) aka observed y - predicted y

What method do you use to check if a distribution or probability is binomial?

BINS:

1. Binary: There only two outcomes (success and failure)

2. Independent: The events independent of one another?

3. Number: There is a fixed number of trials

4. Success: The probability of success equal in each trial

What method do you use to check if a distribution or probability is geometric?

BITS:

1. Binary: There only two outcomes (success and failure)

2. Independent: The events independent of one another

3. Trials: There is not a fixed number of trials

4. Success: The probability of success equal in each trial

n

number of trials

p

probability of success

k

number of successes

Binomial Formula for P(X=k)

(n choose k) p^k (1-p)^(n-k)

Binomial Calculator Function to find P(X=k)

binompdf(n,p,k)

Binomial Calculator Function for P(X≤k)

binomcdf(n,p,k)

Binomial Calculator Function for P(X≥k)

1-binomcdf(n,p,k-1)

mean of a binomial distribution

np

standard deviation of a binomial distribution

√(np(1-p))

Geometric Formula for P(X=k)

(1-p)^(k-1) x p

Geometric Calculator Function to find P(X=k)

geometpdf(p,k)

Geometric Calculator Function for P(X≤k)

geometcdf(p,k)

Geometric Calculator Function for P(X≥k)

1-geometcdf(p,k-1)

Mean of a geometric distribution

1/p=expected number of trials until success

Standard deviation of a geometric distribution

√((1-p)/(p²))

What do you do if the binomial probability is for a range, rather than a specific number?

Take binomcdf(n,p,maximum) - binomcdf(n,p,minimum-1)

how do you enter n choose k into the calculator?

type "n" on home screen, go to MATH --> PRB --> 3: ncr, type "k"

μ(x+y)

μx+μy

μ(x-y)

μx-μy

σ(x+y)

√(σ²x+σ²y)

What does adding or subtracting a constant effect?

Measures of center (median and mean).

Does NOT affect measures of spread (IQR and Standard Deviation) or shape.

What does multiplying or dividing a constant effect?

Both measures of center (median and mean) and measures of spread (IQR and standard deviation).

Shape is not effected.

For variance, multiply by a² (if y=ax+b).

σ(x-y)

√(σ²x+σ²y) --> you add to get the difference because variance is distance from mean and you cannot have a negative distance

calculate μx by hand

X1P1+X2P2+.... XKPK (SigmaXKPK)

calculate var(x) by hand

(X1-μx)²p(1)+(X2-μx)²p(2)+.... (Sigma(Xk-μx)²p(k))

Standard deviation

square root of variance

discrete random variables

a fixed set of possible x values (whole numbers)

continuous random variables

-x takes all values in an interval of numbers

-can be represented by a density curve (area of 1, on or above the horizontal axis)

What is the variance of the sum of 2 random variables X and Y?

(σx)²+(σy)², but ONLY if x and y are independent.

mutually exclusive

no outcomes in common

addition rule for mutually exclusive events

P (A U B)

P(A)+P(B)

complement rule

P(A^C)

1-P(A)

general addition rule (not mutually exclusive)

P(A U B)

P(A)+P(B)-P(A n B)

intersection

P(A n B)

both A and B will occur

conditional probability

P (A | B)

P(A n B) / P(B)

independent events (how to check independence)

P(A) = P(A|B)

P(B)= P(B|A)

multiplication rule for independent events

P(A n B)

P(A) x P(B)

general multiplication rule (non-independent events)

P(A n B)

P(A) x P(B|A)

sample space

a list of possible outcomes

probability model

a description of some chance process that consists of 2 parts: a sample space S and a probability for each outcome

event

any collection of outcomes from some chance process, designated by a capital letter (an event is a subset of the sample space)

What is the P(A) if all outcomes in the sample space are equally likely?

P(A) = (number of outcomes corresponding to event A)/(total number of outcomes in sample space)

Complement

probability that an event does not occur

What is the sum of the probabilities of all possible outcomes?

1

What is the probability of two mutually exclusive events?

P(A U B)= P(A)+P(B)

five basic probability rules

1. for event A, 0≤P(A)≤1

2. P(S)=1

3. If all outcomes in the sample space are equally likely, P(A)=number of outcomes corresponding to event A / total number of outcomes in sample space

4. P(A^C) = 1-P(A)

5. If A and B are mutually exclusive, P(A n B)=P(A)+P(B)

When is a two-way table helpful

displays the sample space for probabilities involving two events more clearly

In statistics, what is meant by the word "or"?

could have either event or both

When can a Venn Diagram be helpful?

visually represents the probabilities of not mutually exclusive events

What is the general addition rule for two events?

If A and B are any two events resulting from some chance process, then the probability of A or B (or both) is P(A U B)= P(A)+P(B)-P(A n B)

What does the intersection of two or more events mean?

both event A and event B occur

What does the union of two or more events mean?

either event A or event B (or both) occurs

What is the law of large numbers?

If we observe more and more repetitions of any chance process, the proportion of times that a specific outcome occurs approaches a single value, which we can call the probability of that outcome

the probability of any outcome...

is a number between 0 and 1 that describes the proportion of times the outcome would occur in a very long series of repetitions

How do you interpret a probability?

We interpret probability to represent the most accurate results if we did an infinite amount of trials

What are the two myths about randomness?

1. Short-run regularity --> the idea that probability is predictable in the short run

2. Law of Averages --> people except the alternative outcome to follow a different outcome

simulation

the imitation of chance behavior, based on a model that accurately reflects the situation

Name and describe the four steps in performing a simulation

1. State: What is the question of interest about some chance process

2. Plan: Describe how to use a chance device to imitate one repetition of process; clearly identify outcomes and measured variables

3. Do: Perform many repetitions of the simulation

4. Conclude: results to answer question of interest

What are some common errors when using a table of random digits?

not providing a clear description of the simulation process for the reader to replicate the simulation

What does the intersection of two or more events mean?

both event A and event B occur

sample

The part of the population from which we actually collect information. We use information from a sample to draw conclusions about the entire population

population

In a statistical study, this is the entire group of individuals about which we want information

sample survey

A study that uses an organized plan to choose a sample that represents some specific population. We base conclusions about the population on data from the sample.

convenience sample

A sample selected by taking the members of the population that are easiest to reach; particularly prone to large bias.

bias

The design of a statistical study shows ______ if it systematically favors certain outcomes.

voluntary response sample

People decide whether to join a sample based on an open invitation; particularly prone to large bias.

random sampling

The use of chance to select a sample; is the central principle of statistical sampling.

simple random sample (SRS)

every set of n individuals has an equal chance to be the sample actually selected

strata

Groups of individuals in a population that are similar in some way that might affect their responses.

stratified random sample

To select this type of sample, first classify the population into groups of similar individuals, called strata. Then choose a separate SRS from each stratum to form the full sample.