Geometry Unit 2 quiz

What does Postulate 1-1

Through any two points, there is exactly one line.

Postulate 1-2

If 2 lines intersect it will be at exactly one point

Postulate 1-3

If 2 plains intersect it will be at exactly one line

Postulate 1-4

Through any 3 non collinear points there is exactly one plain

Postulates / Axiom

Statements that are true without proof

Properties

Algebraic rules used in proofs

Theorems

Statements that can be proven true

Substitution Property

If A = B then A can go in for B in any equation

Transitive property

If A = B and B = C then A=C

Addition, subtraction, multiplication, division, properties of equality

Performing an operation with a constant term on both sides of an equation creates and equivalent equation. 

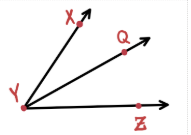
Angle addition postulate

In a given angle ∠XYZ where point Q lies on the interior, m∠XYQ + m∠QYZ = m∠XYZ.

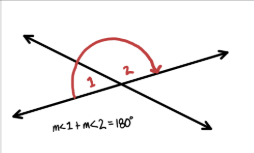
Linear pair theorem

All linear pairs are supplementary

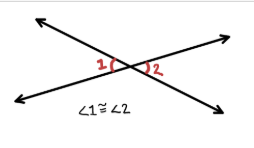
Vertical angles theorem

Nonadjacent angles formed by intersecting lines are congruent

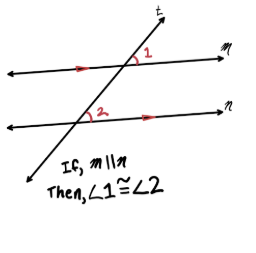
Corresponding angles postulate

If a transversal intersects two parallel lines,  

Then corresponding angles are congruent

Converse Corresponding Angles Postulate

If corresponding angles are congruent,  

Then the lines intersected by a transversal are parallel

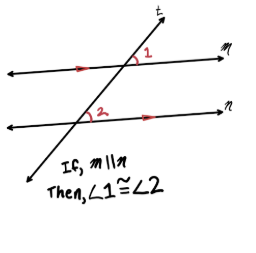
Alternate Interior Angles Theorem

If a transversal intersects two parallel lines,  

Then alternate interior angles are congruent

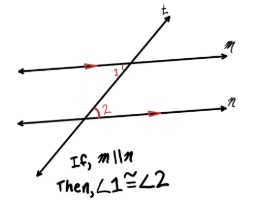
Converse Alternate Interior Angles Theorem

If alternate interior angles are congruent,  

Then the lines intersected by the transversal are parallel

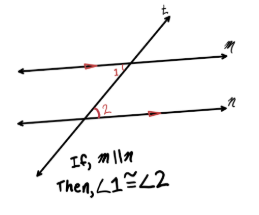
Alternate Exterior Angles Theorem

If a transversal intersects two parallel lines,  

Then alternate exterior angles are congruent

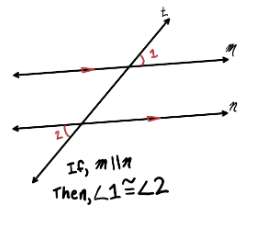
Converse Alternate Exterior Angles Theorem

If alternate exterior angles are congruent,  

Then the lines intersected by the transversal are parallel

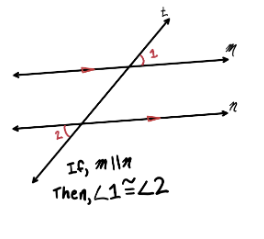
Transversal

A line intersecting a system of lines

Postulate

Reasoning for a belief