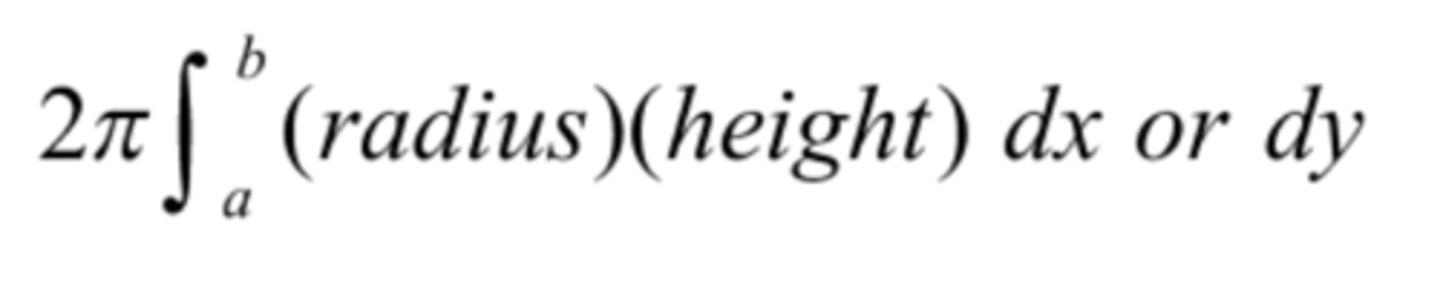AP Calculus AB Need Statements (Cumulative)

x-intercepts/zeroes

y=0 or f(x)=0

y-intercepts

x=0

symmetry to y-axis/even function

f(-x)=f(x)

symmetry to origin/odd function

f(-x)=-f(x)

symmetry to x-axis

-f(x)=f(x)

parallel lines

m₁=m₂

perpendicular lines

m₁ = -1/m₂

domain of √s(x)

s(x)≥0

domain of ln[s(x)]

s(x)>0

domain of 1/s(x)

s(x) ≠ 0

intersection of (f) and (g)

f(x)=g(x)

rational functions zeros

numerator = 0

vertical asymptote

simplify, denom. = 0 and limx→a± f(x)=±∞

horizontal asymptote

degree num. = degree denom., ÷ and limx→±∞ f(x)=a

x-axis asymptote

degree num. < degree denom. and limx→±∞ f(x)=0

slant asymptote

degree num. = 1 + degree denom., ÷

limit of a piece function

limx→a⁺ f(x) = limx→a⁻ f(x)

continuity at x=a

limx→a f(x) = f(a)

continuity of a piece function

limx→a⁺ f(x) = limx→a⁻ f(x) = f(a)

derivative by definition

f'(x) = lim∆x→0 (f(x+∆x)-f(x))/∆x

f'(c) = limx→c (f(x)-f(c))/(x-c)

rate of change

f'(x)

slope of a curve

f'(x)

slope of a tangent

f'(x)

equation of a tangent

y-y₁ = f'(x₁)(x-x₁)

slope of a normal

mₙ = -1/mt = -1/f'(x)

horizontal tangent

f'(x)=0

vertical tangent

f'(x)=non zero constant/0

average rate of change

∆y/∆x

PVA position

s(t)

PVA velocity

v(t)=s'(t)

PVA acceleration

a(t)=v'(t)=s''(t)

Particle at rest

v(t)=0

Particle moving right

v(t)>0

Particle moving left

v(t)<0

Particle changes direction

v(t) changes sign

Particle total distance traveled

|s(t₁)-s(tc)+|s(tc)-s(t₂)|, where tc=time particle changes direction

Particle average velocity

∆s/∆t = displacement/time change

Particle speed

|v(t)|

critical number (c)

f'(x) = 0 or f'(x)DNE

relative max.

1st Deriv. Test: f'(x) changes from positive to negative at x=c, 2nd Deriv. Test: f"(c)<0

relative min.

1st Deriv. Test: f'(x) changes from negative to positive at x=c, 2nd Deriv. Test: f"(c)>0

f is increasing

f'(x)>0

f is decreasing

f'(x)<0

abs max. on [a,b]

compare the y-value(s) of relative max's with f(a) and f(b)

abs min. on [a,b]

compare the y-value(s) of relative min's with f(a) and f(b)

concave up

f"(x)>0 or f'(x) inc.

concave down

f"(x)<0 or f'(x) dec.

point of inflection

f"(x) changes sign, tangent must exist or f'(x) changes from increasing to decreasing, or from decreasing to increasing

area under curve

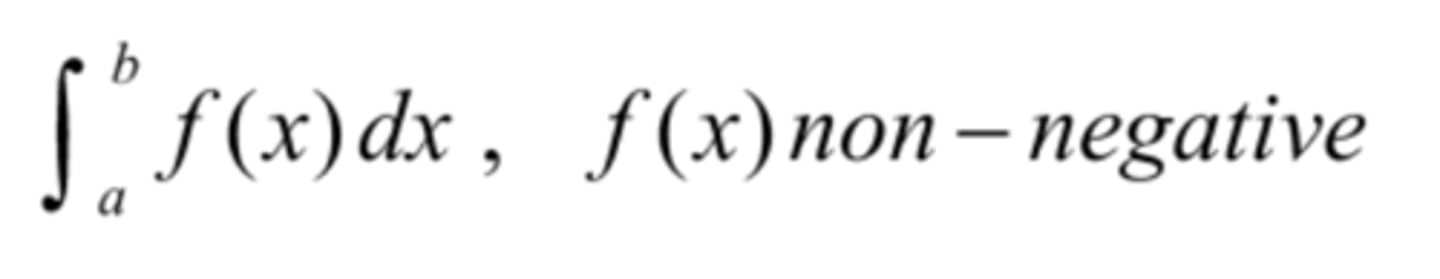
area between curves

average values

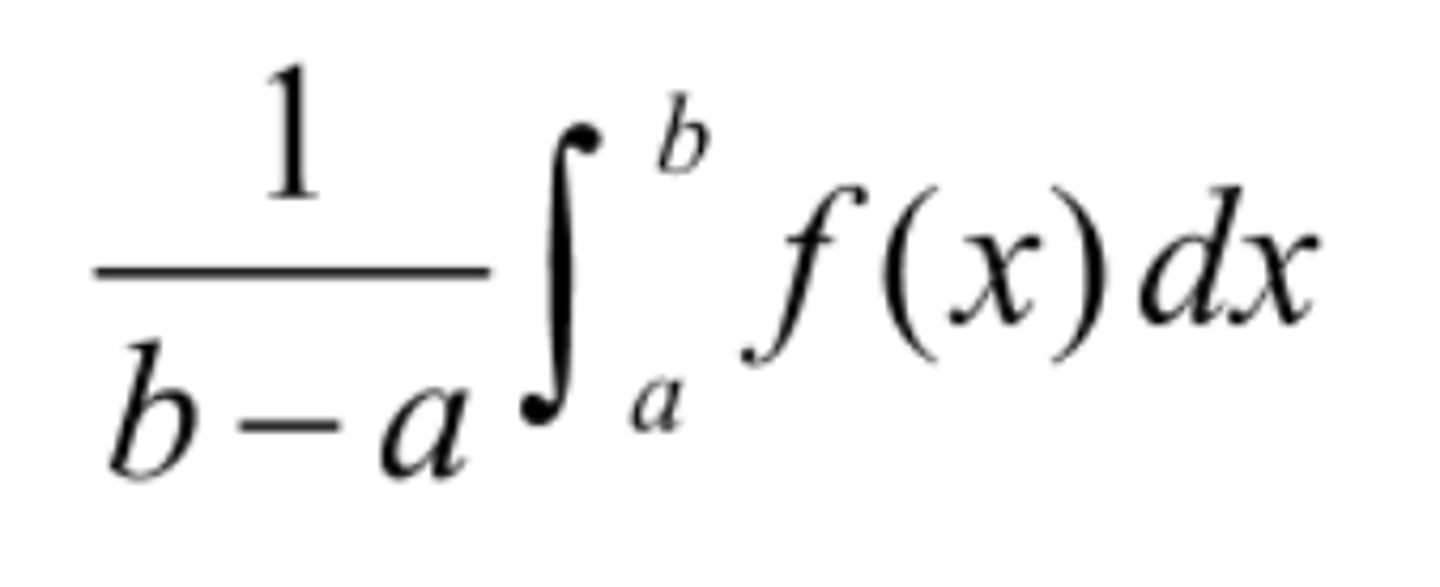
Trapezoidal rule: From a to b ∫f(x)dx ≈

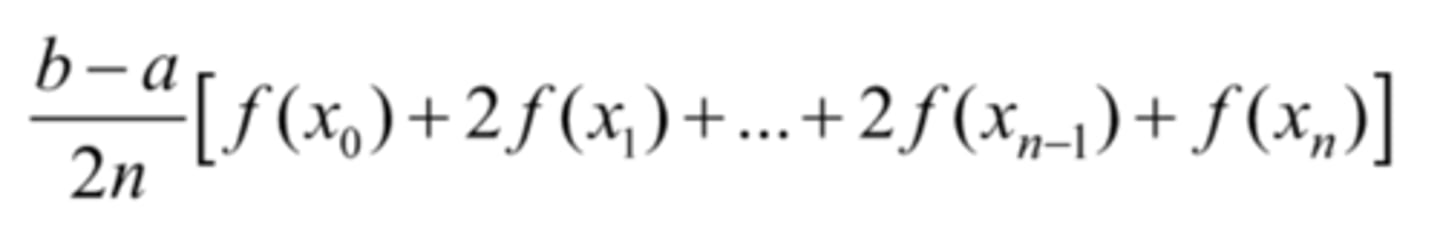
volume by disks

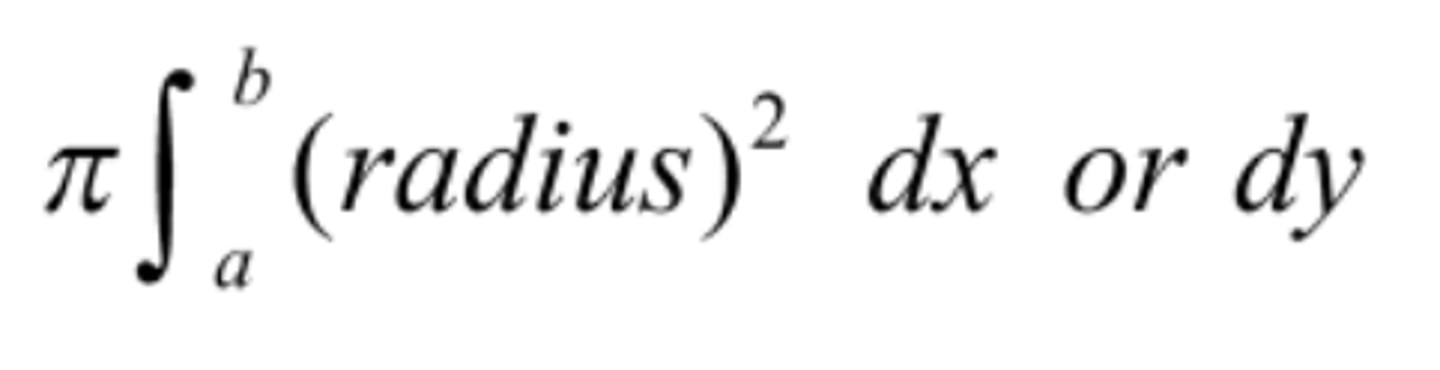
volume by washers

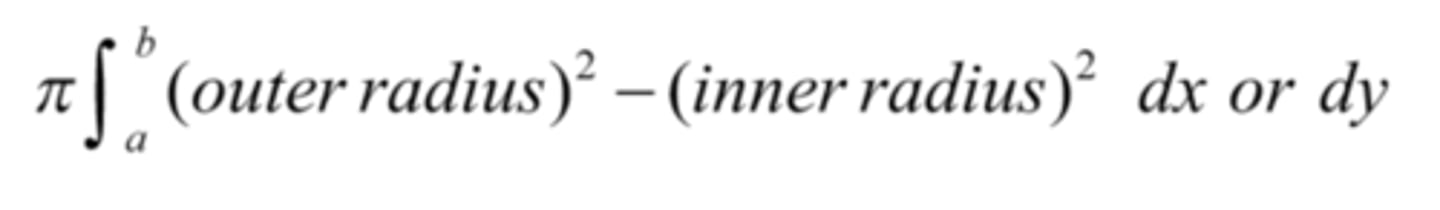
volume by shells