NURS 211 Statistics Full review

nominal, ordinal, interval, ratio

What are the 4 Levels of Measurement?

Hint: N.O.I.R

Categorical variable

A variable that has a finite number of classification groups/ categories, which are usually qualitative in nature

Continuous variable

A variable that has a infinite number of potential values, with value being measured falling somewhere on a continuum containing in-between values.

Empirical method

What method is a way of gathering information through systematic observation and experimentation?

Parameter

___________ is a measurable characteristic of a population

Statistic

_____________ is an estimate derived from a sample

- numerical measurement describing some characteristic of a sample

Estimate

_____________ is a preliminary approximation

Qualitative measure

What measure describes or characterizes an attribute?

- data in words

ex. The day is "warm" or "cold"

Quantitative measure

What measure reflects a numeric amount?

- data in numbers

ex. writing down the temperature for the day

Nominal

Marital status: you're either married (together)/ divorce(not together) Is an example of what level of measurement?

Hint: sounds like "Name/Nom"

- no order, either has it or doesn't

Ordinal

Pain scale, stress scale (ex: low, medium, high stress level) is an example of what level of measurement?

Hint: sounds like "Ordered"

- no equal interval between the values

- Comparison between smaller value to bigger value

Interval

Temperature and Student tests are examples what level of measurement?

- Ordered,

- Equal ___________ between values

- No true "zero"

Ratio

Tests such as: Blood pressure, (if patient's BP is 0 then they're in trouble, heart isn't beating, dead = true zero),

- blood sugar, renal function, glascow coma scale, BMI etc. Are examples of what level of measurement?

-Ordered

- Equal interval between values

- Has a true zero

- Very precise, accuracy (best for healthcare)

- bodily measures ex.) there can be 0 weight gain

Dependent variable

The _________________ is the outcome factor.

- The variable that may change in response to manipulations of the independent variable.

- Depends on independent variable

Independent variable

The _______________ is the variable that experimenter can change

- influences dependent variable.

Mean

____________(M)

- average,

[Calculation: add all numbers then, divide by number of values]

Ex: Videos, Reading

- Good for interval and ratio data

- Best measure for symmetrical distribution of data

Median

___________- middle (Medium)

[Calculation: Arrange in order,

Number is odd = middle value

Number is even = mean of the middle values]

Ex: Odd (reading), Even (videos)

- Works for Ordinal, interval and ratio data

- Good for asymmetrical data distribution

- Not appropriate for nominal data

Mode

___________ - sounds like "Most", most frequent number

[Calculation: arrange number in order, count the number that shows up most frequently]

- Only appropriate for nominal data

- Can also be used for ordinal, interval and ratio data

(Patients score - Sample mean) ÷ (Standard deviation/ SD)

Z-score

Points out outlier patients/ defiant patients

Ex) patients way below or above a scale

captures how much people deviate from the mean/defy the average

What is the formula for Z-scores?

Formula:

___________ ÷ ___________ = Z-score

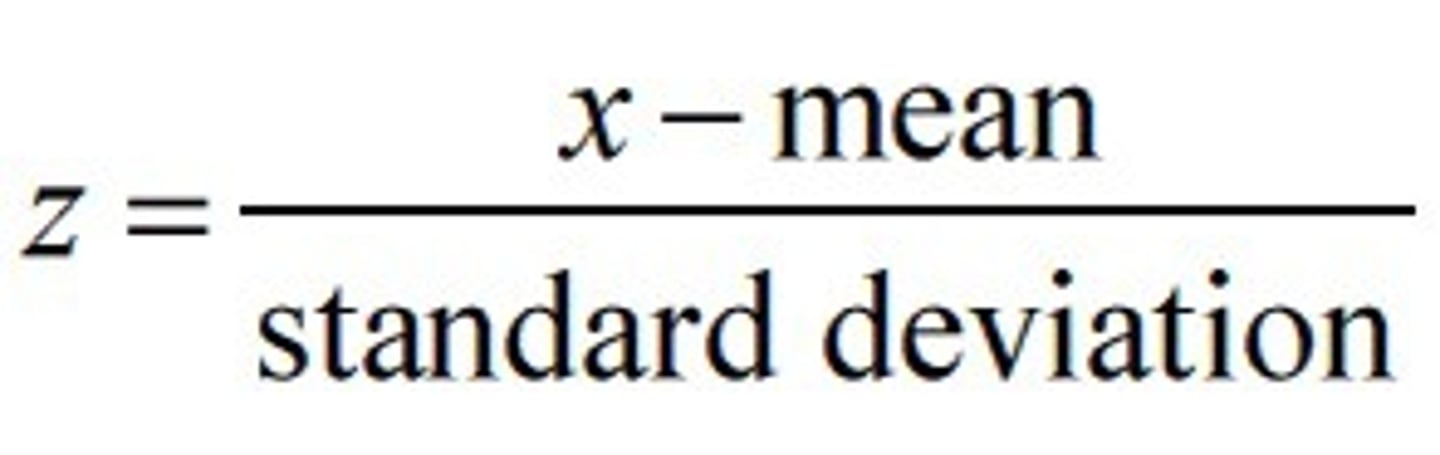
Normal distribution

What kind of distribution has the:

- Measures of central tendency (mean, median, mode) all fall in the same midline point? (ALL EQUAL)

- Bell shaped

- Has a mean of 0 and Standard deviation of 1

Standard Deviation (SD)

- The average distance that values in a distribution are from the centre

- Indicates how many far a value is from the mean value.

Low SD = values are close to the mean (homogenous sample)

High SD = values spread out over a large range (heterogenous sample)

What measures how much variation exists in distribution?

Probability

The chance that a particular outcome will occur

ex.) 75 students in class and 69 are female and 6 are males - what is ___________ of a male student being randomly selected from a seminar group?

[6/75 = 0.08 x 100 = 8%]

0.05 or 95%

Alpha = the probability of incorrectly rejecting the null hypothesis or making a type 1 error

The significance level of Alpha is usually: ___________.

0.20 or 20%

Beta = the probability of accepting the null incorrectly or making a type 2 error

The significance level of Beta is usually: __________.

1 - 80 = beta

How would you calculate Beta if the power of the study is 0.80?

p-value

the probability of finding the outcome you observed if the null hypothesis is true

- The probability you got your finding due to chance (don't want result to be due to chance so p-value should be low)

Low value = low probability

High value = high probability

Reject the null hypothesis

If the p-value is LESS than the alpha, you should _____________.

Fail to reject the null hypothesis

If the p-value is GREATER than the alpha, you should ____________.

- there is no relation

Probability Sample

______________ is a technique where the probability of selecting each subject is known (Randomized)

Simple Probability Sampling

______________ = All individuals in a population have an equal probability of being selected

ex) Randomly picking from a CARNA list

Systematic Probability Sampling

______________ = Probability sampling involving selecting subjects according to a standardized rule

ex) Picking every 5th person in a population

Stratified Probability Sampling

______________ = A probability sampling technique where a researcher begins by identifying subgroups (or strata) and then randomly samples from each subgroup.

ex) Identifying nurses that have worked for 1 year and randomly selecting 20% of your sample from this group

Cluster Probability Sampling

________________ = Randomly selecting a group or unit rather than a individual

ex) Geography, randomly selecting nurses from Rural hospitals or Urban hospitals

Non-probability sampling

______________ are methods in which subjects DO NOT have the same chance of being selected (NOT Randomized)

Convenience probability sampling

______________ = Selecting & collecting data from a population that is available

ex) Doing a study on the nurses in your clinical group

Quota probability sampling

______________ = Selecting proportion of the sample for different subgroups.

- Similar to Stratified sampling but is NOT randomized

ex) After deciding on your proportion of the sample, you collect data continuously until you meet your set goal (until you reached your quota)

Range

_____________ is the difference between maximum and the minimum values in a distribution

Central Limit Theorem

- states that the sampling distribution of the sample means approaches a normal distribution as the sample size gets larger — no matter what the shape of the population distribution.

- If the number in your sample is around 30 your data will likely approximate to normal distribution

30

Central Limit Theorem

→ if the number in your sample is around _______ your data will likely approximate to normal distribution.

Sample mean will be approximately normally distributed for larger sample sizes, regardless of the distribution from which we are sampling.

As you take more samples, especially large ones, your graph of the sample means will look more like a normal distribution.

What is the ideal number of people to have in a study?

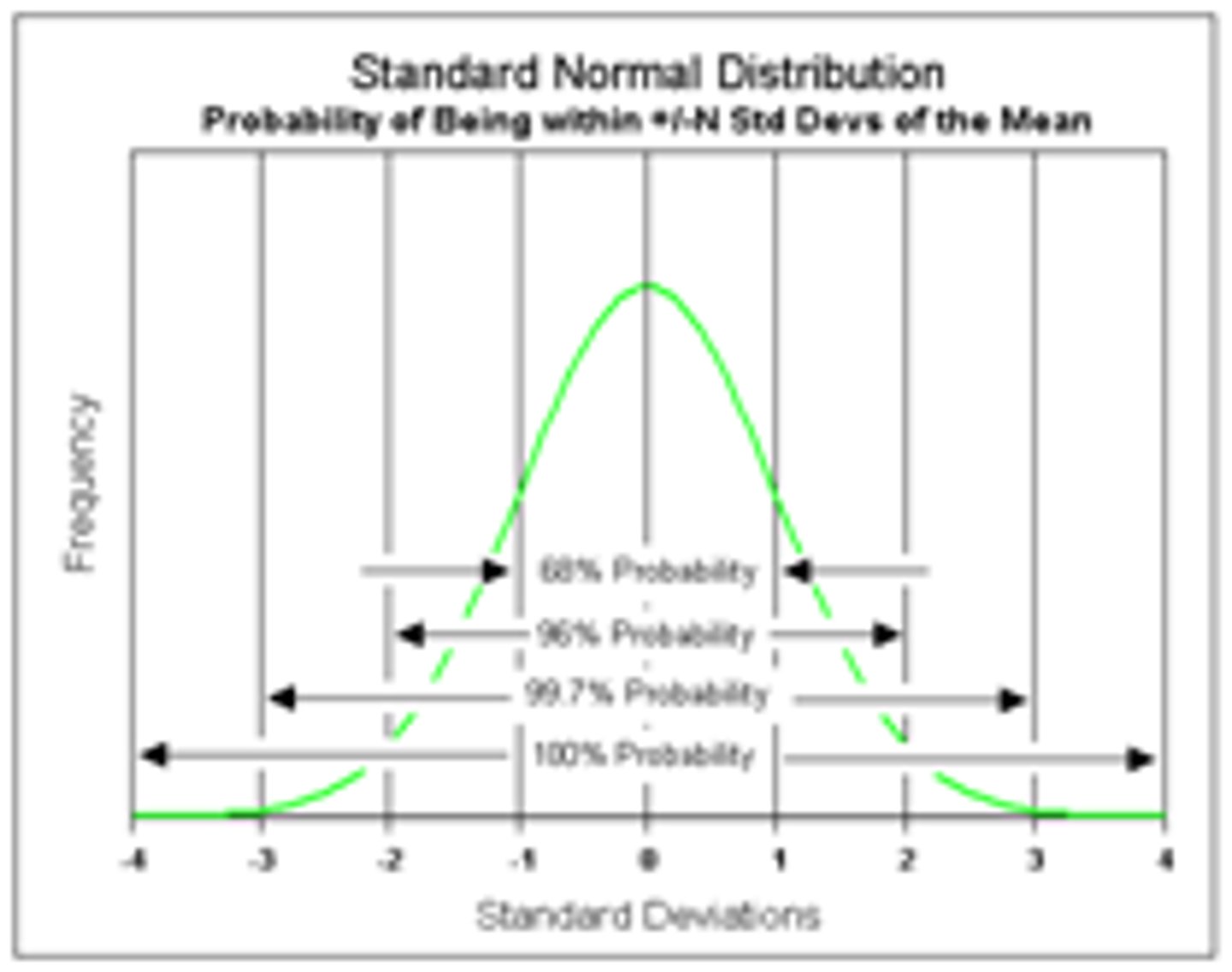
68-95-99.7 rule

in a normal model, about 68% of values fall within 1 standard deviation of the mean

about 95% fall within 2 standard deviations of the mean

99.7% fall within 3 standard deviations of the mean

--> More than 3 SD above or below average is "Outlier" or "weirdo"

anyone deviates that far out should be investigated further

Inclusion criteria

characteristics a subject must have to be eligible to participate in a study

Exclusion criteria

Characteristics that eliminate a potential subject from the study

Sampling error

The differences between the sample and the population that occurs due to randomization or chance

- Errors made by chance alone

Sampling bias

Systematic error made in the sample selection that results in a nonrandom sample

- something that has gone wrong while conducting a sample

- Error you're making on purpose

- Errors YOU make that result in a non-random sample

Data collection error

Data handling error (made when processing data)

Reporting error (reporting something untrue)

What are three examples of sampling bias?

1.

2.

3.

Effect size

<.30, .30-.50, >.50

The extent to which a difference or relationship exists between variables in a population (size of the difference you are attempting to find)

Weak Effect _______ (Want LARGER sample size)

Moderate Effect _______

Large Effect _______ (Want SMALLER sample size)

Sample size

The number of subjects used in an experiment or study. - Generally, the larger the better.

- Calculated by: Power analysis

Smaller sample size

- less info

- wider confidence intervals

- greater chance of making a type 2 error

Larger sample size

- more info

- sampling error reduced

- narrow confidence interval

- greater chance of making a type 1 error

Confidence interval

Variation of population

Size of sample

- Communicates how accurate our estimate is likely to be

What two things affects the width of ________________?

1.

2.

Type 1 error (alpha)

- Incorrectly REJECTING the null hypothesis

- Rejecting null hypothesis when it is true

- When data is true => reject data

ex) Think you got the cure for cancer but you actually don't.

Type 2 error (beta)

- Incorrectly ACCEPTING the null hypothesis

- Missing an association that is really there

- When data is false => accept data

ex.) Got the cure for cancer but then got insecure and trashed it.

Type 2 error is 4 times more serious

Which type of error is more serious to make in a healthcare setting and why?

20% chance of committing vs. 5%chance of committing

Power

______________ is the ability to find a difference/association when one really exists

- has a significance level of usually: 0.80 or 80%

- When sample size increases = Power of study is increased = likelihood of correctly rejecting null hypothesis also increases.

Reliability

What is it called when your measurement tool is consistent or repeatable?

- Measure has good reproducibility

Test-retest reliability

- Correlation of the scores obtained by a measure at two different times

- Participants are given the same test at 2 different times

Correlation between test 1 and test 2 (testing twice)

Inter-rater reliability

Correlation of measurements observed by two or more raters

Ex. asking two people about their pain and they say around the same value

Internal consistency

All the items in a survey tool measure the same concept (i.e., coping).

Equivalence reliability

Different forms of your survey tool yield matching (consistent) scores.

Validity

- The extent to which a measurement measures what it intends to measure

Ex. a questionnaire about self-esteem should be capturing self esteem, not other concepts like extroversion

Divergent validity

- The degree to which results of a measure do NOT correlate with other variable or measures

Covergent validity

- a determination that the test results obtained are similar to the results obtained with another previously validated test that measures the same thing

Predictive validity

Measurement of how accurately an instrument suggest future outcomes/behaviours

- How scores predict a health outcome

ex) People with high serum cholesterol scored low on exercise

Construct validity

the extent to which variables measure what they are supposed to measure

- Do the items in your tool 'stick together' in an expected way.

Yes, a measurement can be Reliable and not Valid BUT CAN'T be Valid and not Reliable.

- For something to be valid, it needs to be reliable and accurate

Can a measurement be Reliable but not Valid?

Dependant samples

- When members of one sample are related to members of the other sample.

-NOT random

-Sample B depends on the result of sample A because they are related.

ex.) Sample A is taken from husbands and Sample B is taken from their wives. (related)

Independent samples

- RANDOM, Unrelated

- There is no relationship between sample A and B

Null

Nothing, Not different

No difference or association between variables that is any greater or less than would be expected by

chance.

Alternative

Opposite of the null

Alternative POV

Usually the relationship or association or difference that the researcher actually believes to be present.

Parametric statistics

What kind of statistics need....

- Needs to be ratio or interval LOM

- Normally distributed

- No outliers

- Homogeneity of variance

- Sample sizes larger than minimum for many nonparametric tests

______________________

- More powerful, more likely to detect a difference that truly exists

Less likely to make a type 2 error

Nonparametric statistics

Random independant Samples

______________ - small sample, non normally distributed date

- More conservative

- Less statistical power

What kind of statistic is more likely than a parametric test to produce type 2 error?

One-tailed test

A hypothesis test in which rejection of the null hypothesis occurs for values of the test statistic in one tail of its sampling distribution.

Two-tailed test

A hypothesis test in which rejection of the null hypothesis occurs for values of the test statistic in either (both) tails of its sampling distribution.

Chi-square (x^2)

2 independent samples of nominal or ordinal level data

- Looks for associations or relationships between groups

-Highly sensitive to sample size

- Samples should be Random & Independent

Change in (observed - expected)^2 / expected

What is the formula for Chi-square?

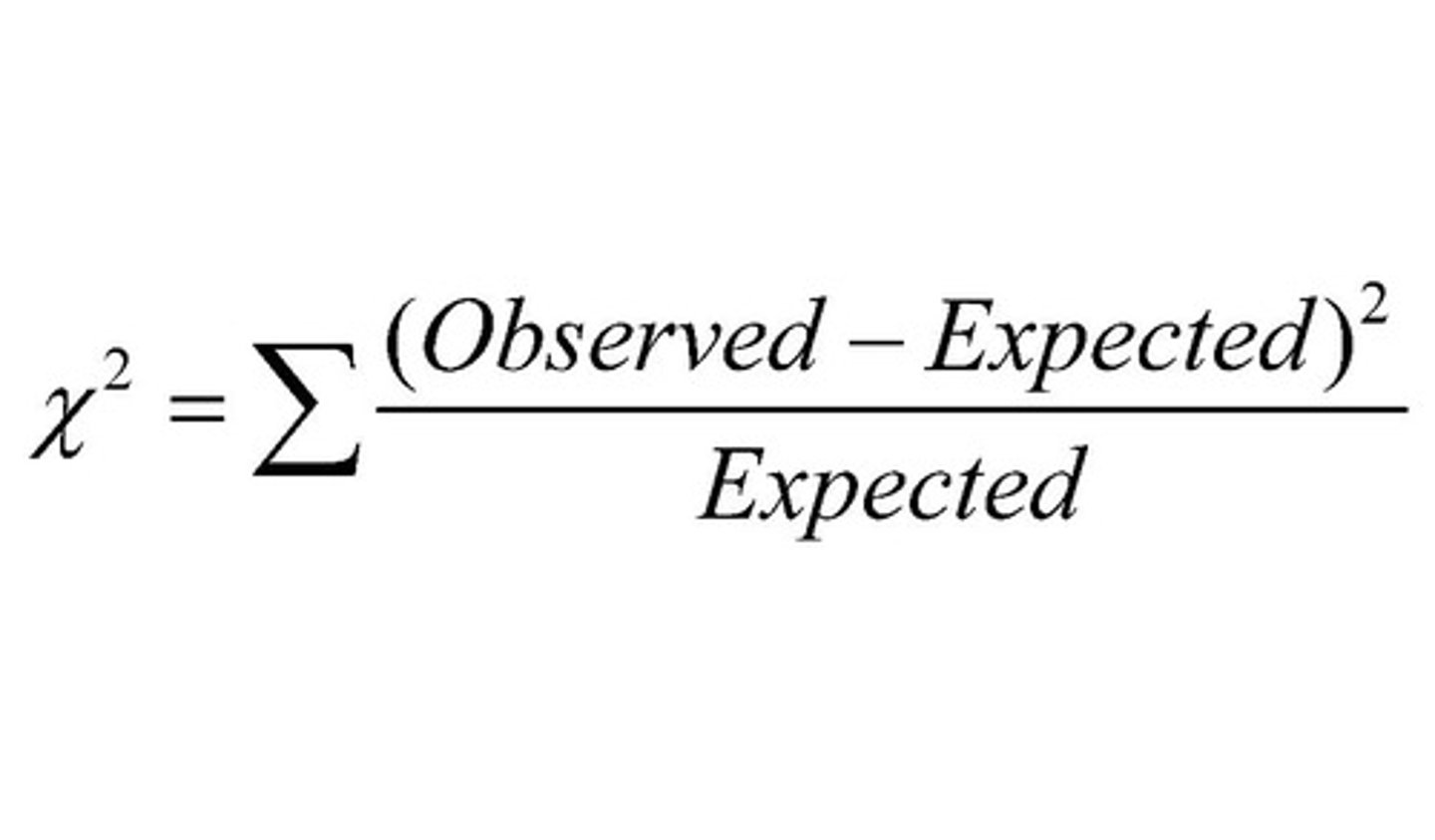
Expected Frequency

____________ = (Row total x Column total)/ Grand total

Reject the Null hypothesis

(P-value is less than 0.05/alpha)

- There is an association

If X2 result has a p-value that is LESS than alpha you should....

Fail to reject the null hypothesis

(P-value is greater than 0.05/alpha, Ex) p-value is 0.09)

- There is not enough statistical strength to say the variables are not related.

If X2 has a p-value GREATER than the alpha you should....

Degrees of freedom (df)

the values that are "free to be unknown"

(df = n-1 )

df for a 2x2 is always "1"

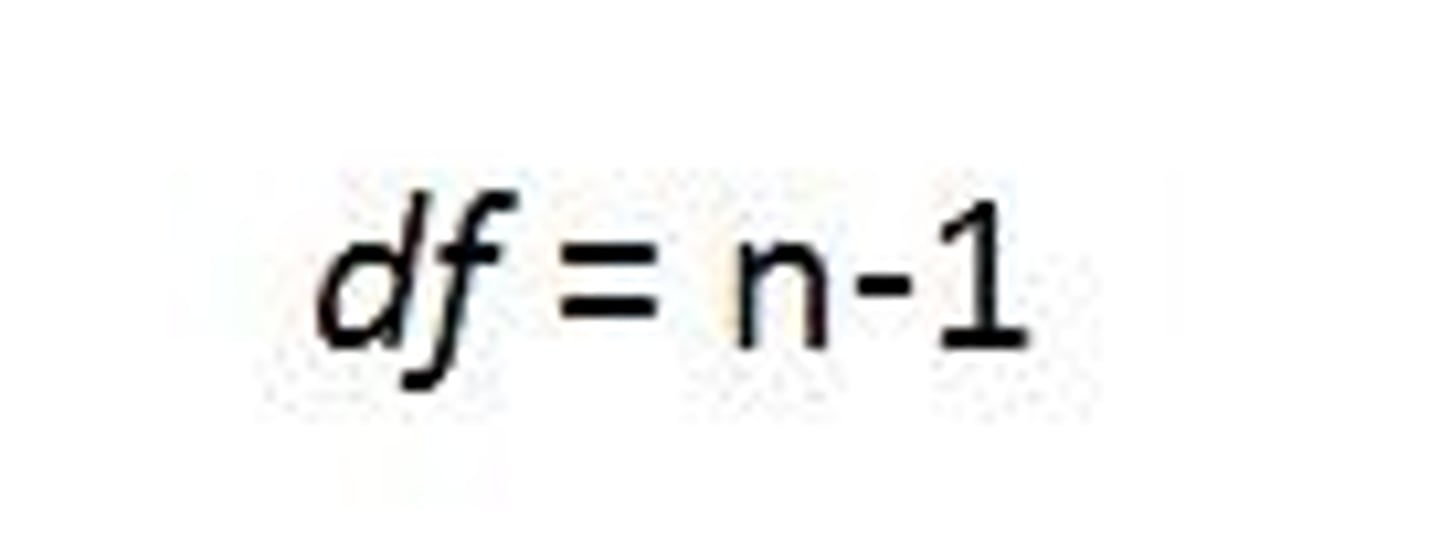
Student t-test

A test used when you are looking for a difference in the MEAN VALUE of an interval-level or a ratio-level variable.

- Interval or Ratio level

- Two samples

- Random and independent samples

Degrees of Freedom (t-test)

DF = [(# of total subjects in sample1) + (# of total subjects in sample2)] - 2

t-value

Mean difference / Standard error

Analysis of Variance (ANOVA)

A test used when comparing the means from a single dependent variable among TWO OR MORE groups of samples

-Detect differences between continuous variables when there are two or more groups

Variance

differences, how much that persons score is different between the average score.

- The square of the standard deviation

Levene's Test for Equality of Variances

A method that tests the null hypothesis that the variances in the two groups being compared are NOT DIFFERENT

- tests for the homogeneity of variance (variances are somewhat similar)

Levene's test

If _________ ______ has a significant p-value, you do not assume equal variances.

If the _________ ______ does not show a significant p-value, you can assume equal variances.

F ratio

Compares between-groups variance to within-groups variance

Formula:

F= (Between group variation) / (Within group variation)

Can also think of it as:

F = (Treatment / sampling error)

What is the ideal F-ratio?

F-ratio greater than 1.0 is ideal --> Larger F-ratio is more likely to have a significant p-value

- 'between group' variation should be higher

- (Numerator should be bigger than the denominator)

Appropriate use of ANOVA (4)

1. Sample should be INDEPENDENT (ideally random)

2. Measure must be in INTERVAL or RATIO level

3. Sample should be NORMALLY DISTRIBUTED

4. HOMOGENEITY of variance (scores need to vary similarly among the 3 groups)

Repeat-measures ANOVA

Examines a change over time in the same sample population

- one group with outcomes at multiple points in time

- Useful for dependent samples

- Compound symmetry

- Be aware of Latency effects and Carry over effects.

What are Assumptions used for Repeat ANOVA?

Compound symmetry

measurements are correlated and of equal variances

Latency Effects

When a subject is being exposed to more than one treatment overtime and order of the treatment effects the outcome.

Carry over effects

When previous treatments continue to have an effect in the next treatment

Correlation

A measure of the relationship between at least two variables

- Strength of relationship

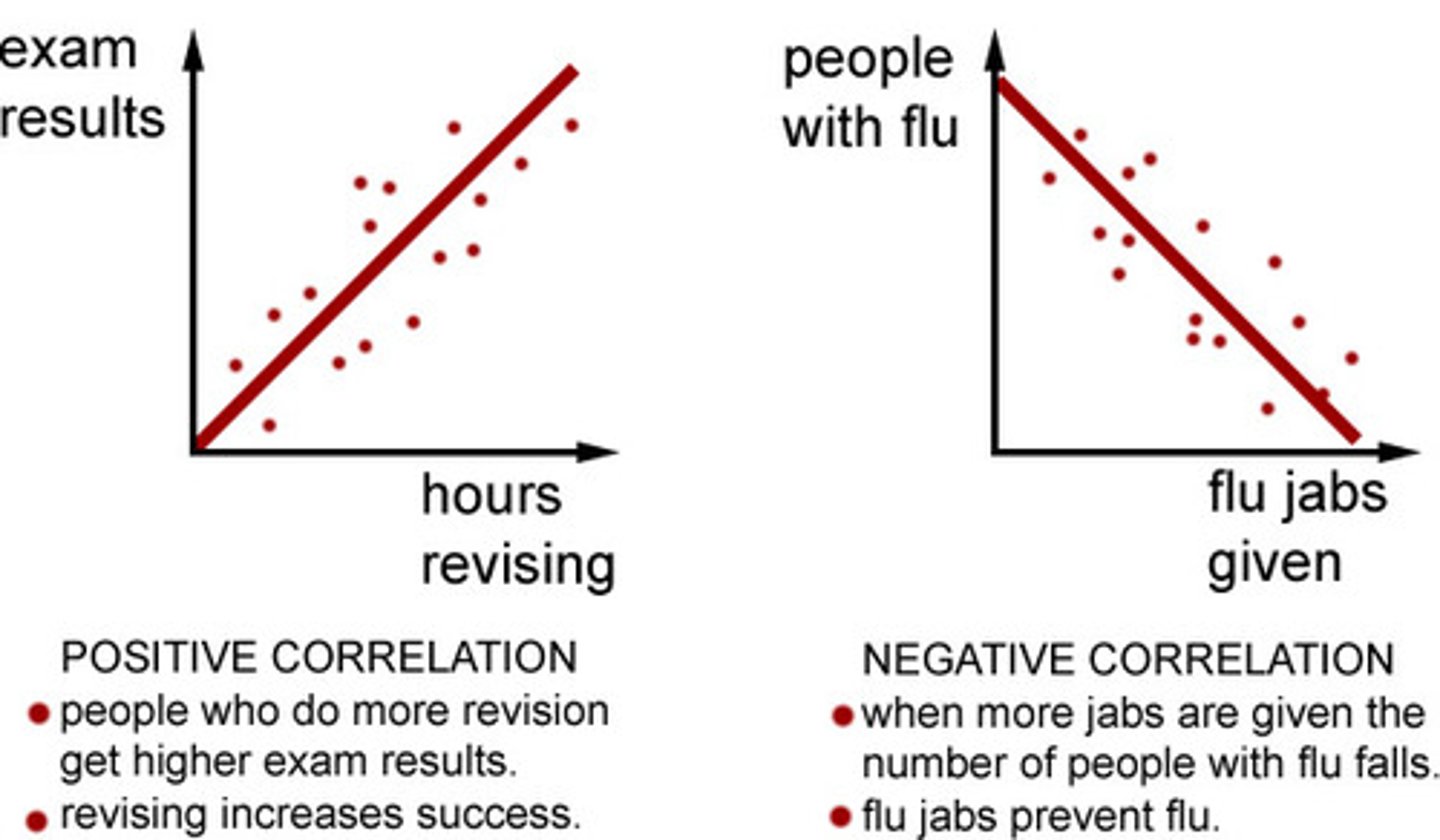
Direction of Relationship

Is either positive or negative

Positive: Two variables tend to increase or

decrease TOGETHER

Negative: Two variables tend to move in OPPOSITE directions

Pearson's correlation coefficient (Pearson's r)

Used when looking for a relationship between two variables that are:

- Normally Distributed

- Interval or Ratio level

Spearman correlation coefficient (⍴)

Used to determine if there is a relationship between two variables but don't meet Pearson's assumptions:

- NOT Normally distributed

- Ordinal, Interval or Ratio level

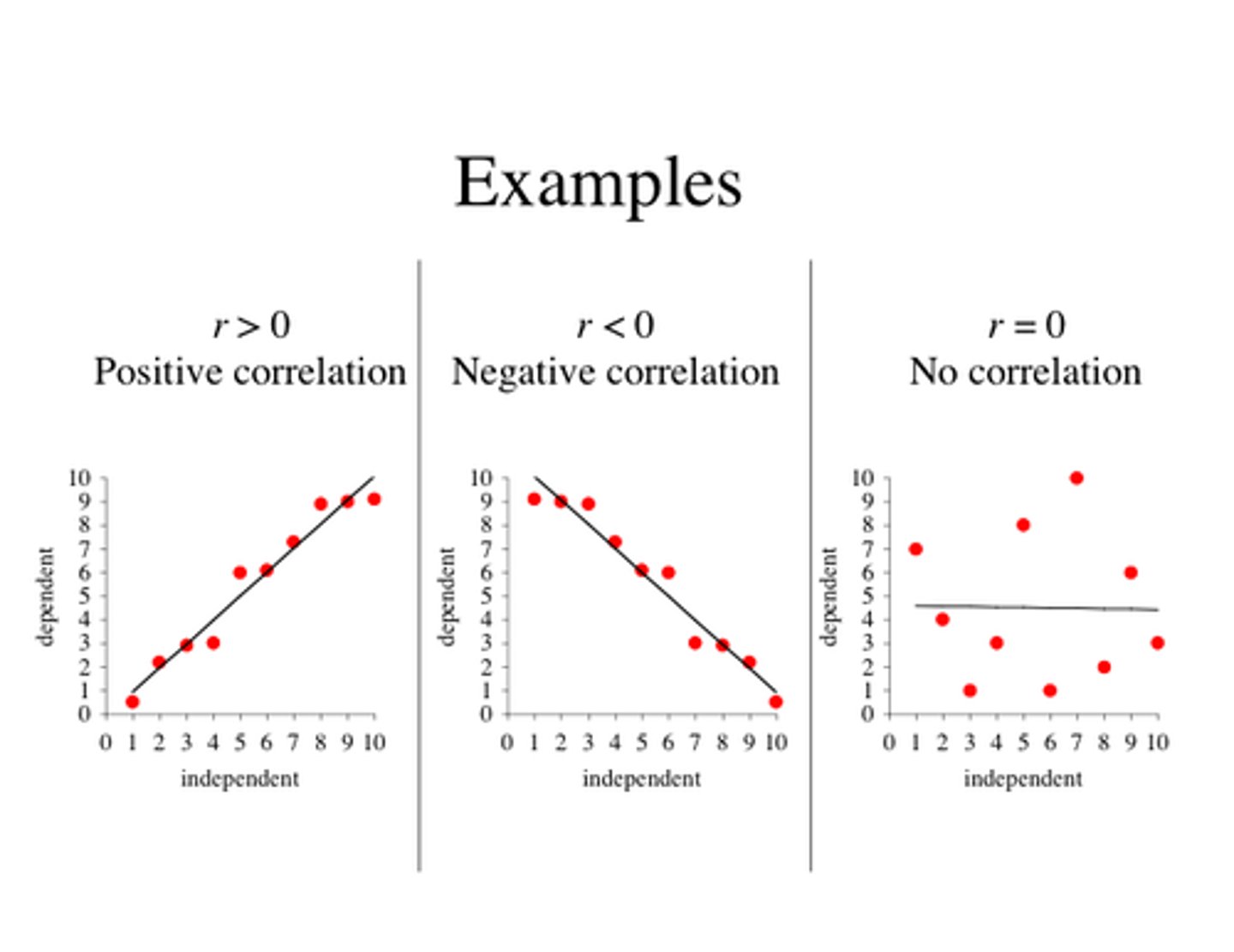
Correlation Coefficient

Always Range From -1 to +1

-1 = Perfect negative relation

0 = No relation

+1 = Perfect positive relation

Positive correlation: Coefficient is also Positive

- Ex) Time studying for an exam and exam grade is positively correlated

Negative correlation: Coefficient is also Negative

- Ex) When Smoking increases, Life expectancy decreases & vice versa

Percentage of Variance

The amount of variance in one variable that is explained by the second variable.

Formula: Coefficient of determination x 100

- ** r > 0.3 is considered clinically important