AP Calculus AB Chapter 1

Average Rate of Change

The slope of the secant line between two points

Continuity

When a function has no holes, jumps, or vertical asymptotes

Discontinous

When a function has a jump, hole, or vertical asymptote

Horizontal Asymptote

A horizontal line that a function's graph approaches as the inputs reach negative or positive infinity

Infinite Discontinuity

When a graph has a vertical asymptote

Instantaneous Rate of Change

The rate of change at a given point

Intermediate Value Theorem

For a continuous function on a closed interval [a, b], if L is any value between f(a) and f(b), then there must be at least one value c within the interval [a, b]

Jump Discontinuity

When two parts of a function don't meet up and have to jump, not removable

Left-Hand Limit

The limit of a function when approaching from the left

Limit of a Function

Describes the value that the function approaches as the input approaches a specific point

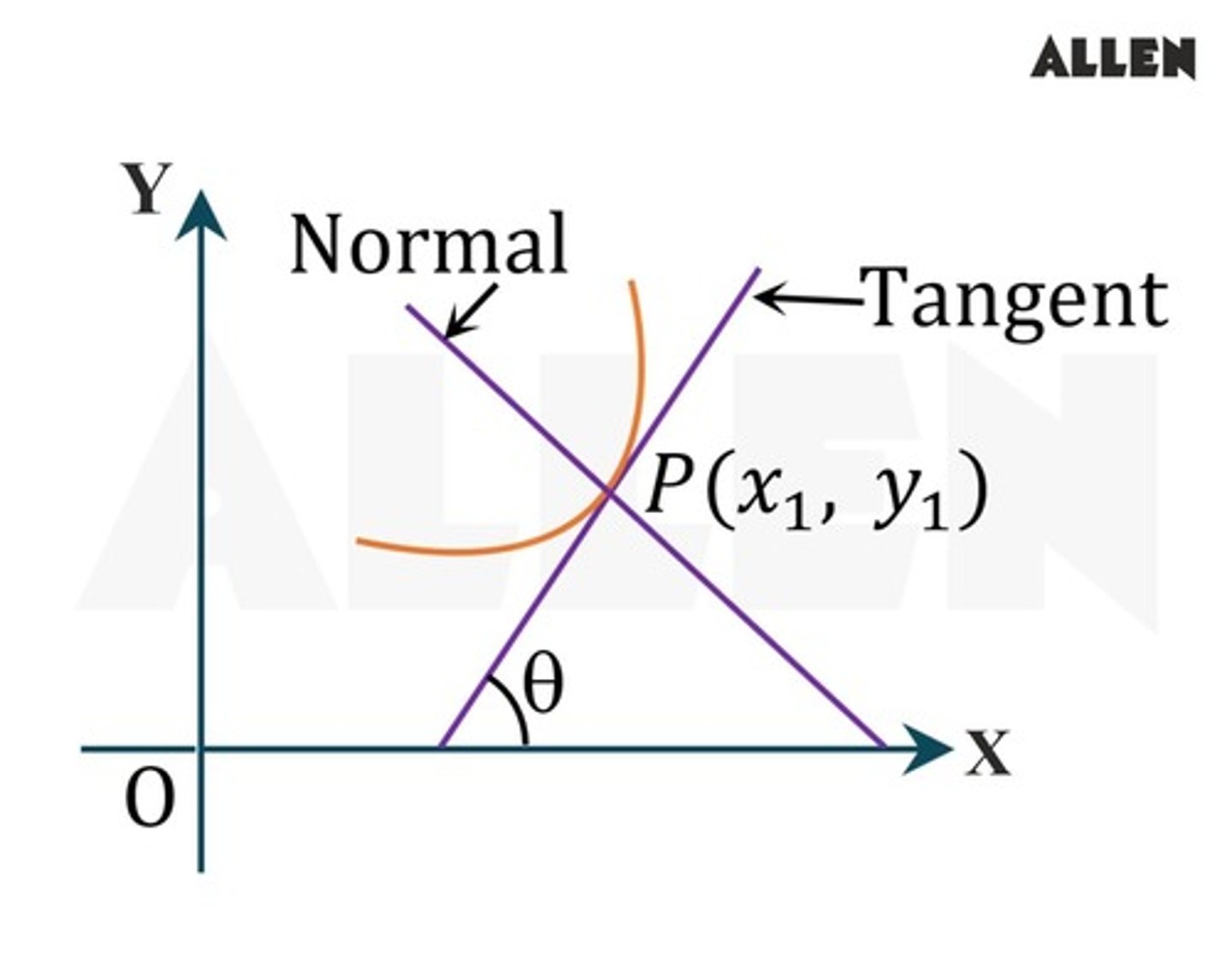
Normal to a Curve

A straight line that is perpendicular to the tangent line to the curve at that same point

Oscillating Discontinuity

When a graph approaches two values simultaneously

Removeable Discontinuity

When a graph has a hole that can be plugged to make the function continuous

Right-Hand Limit

The limit of a function when approaching from the right

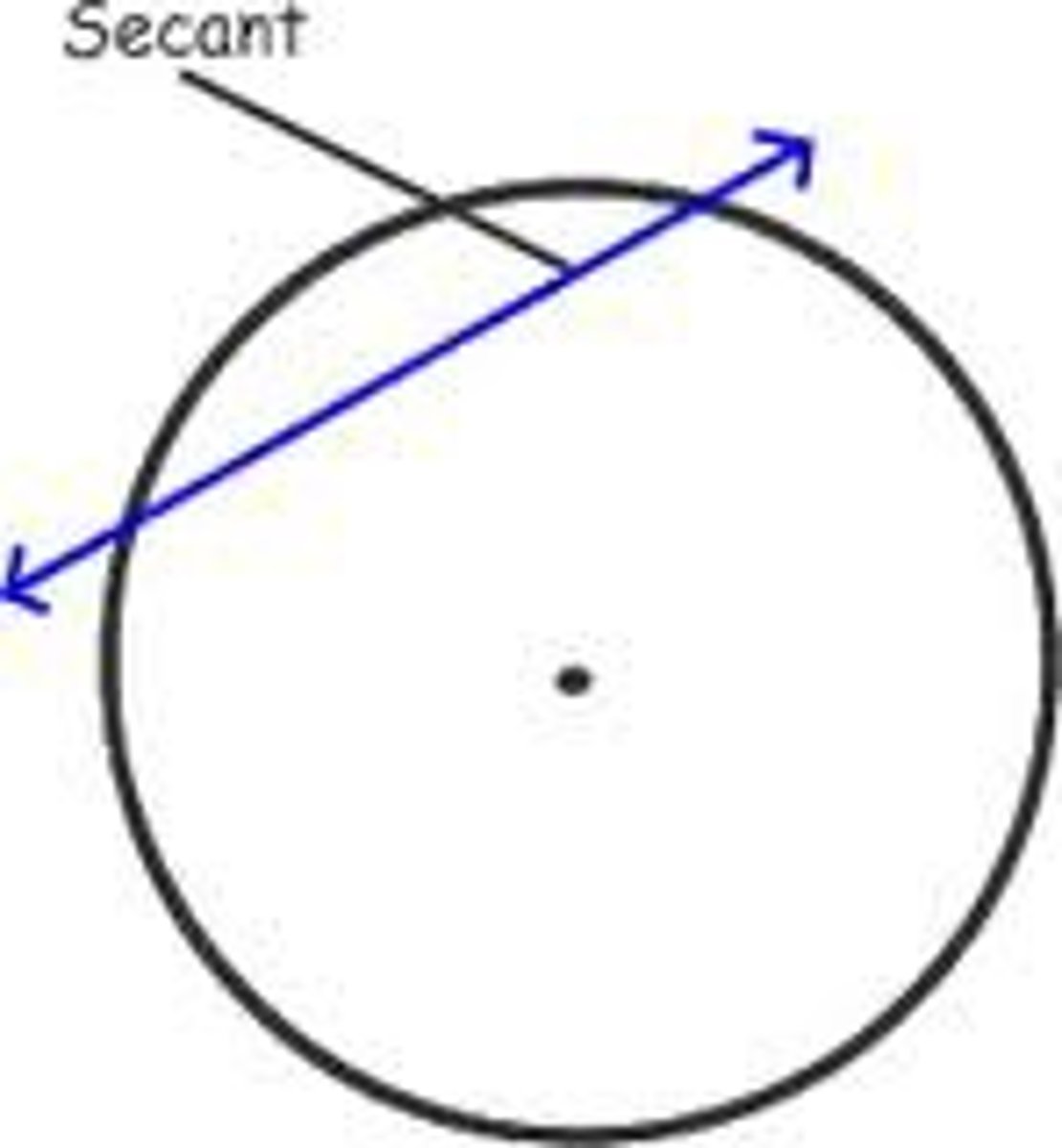
Secant to a Curve

A straight line that intersects the curve at two or more distinct points

Slope to a Curve

Represents the instantaneous rate of change of the variable on the vertical axis (y) with respect to the variable on the horizontal axis (x)

Tangent Line to a Curve

A straight line that touches a curve at a single point

Two-Sided Limit

The limit when approaching from both the left and the right

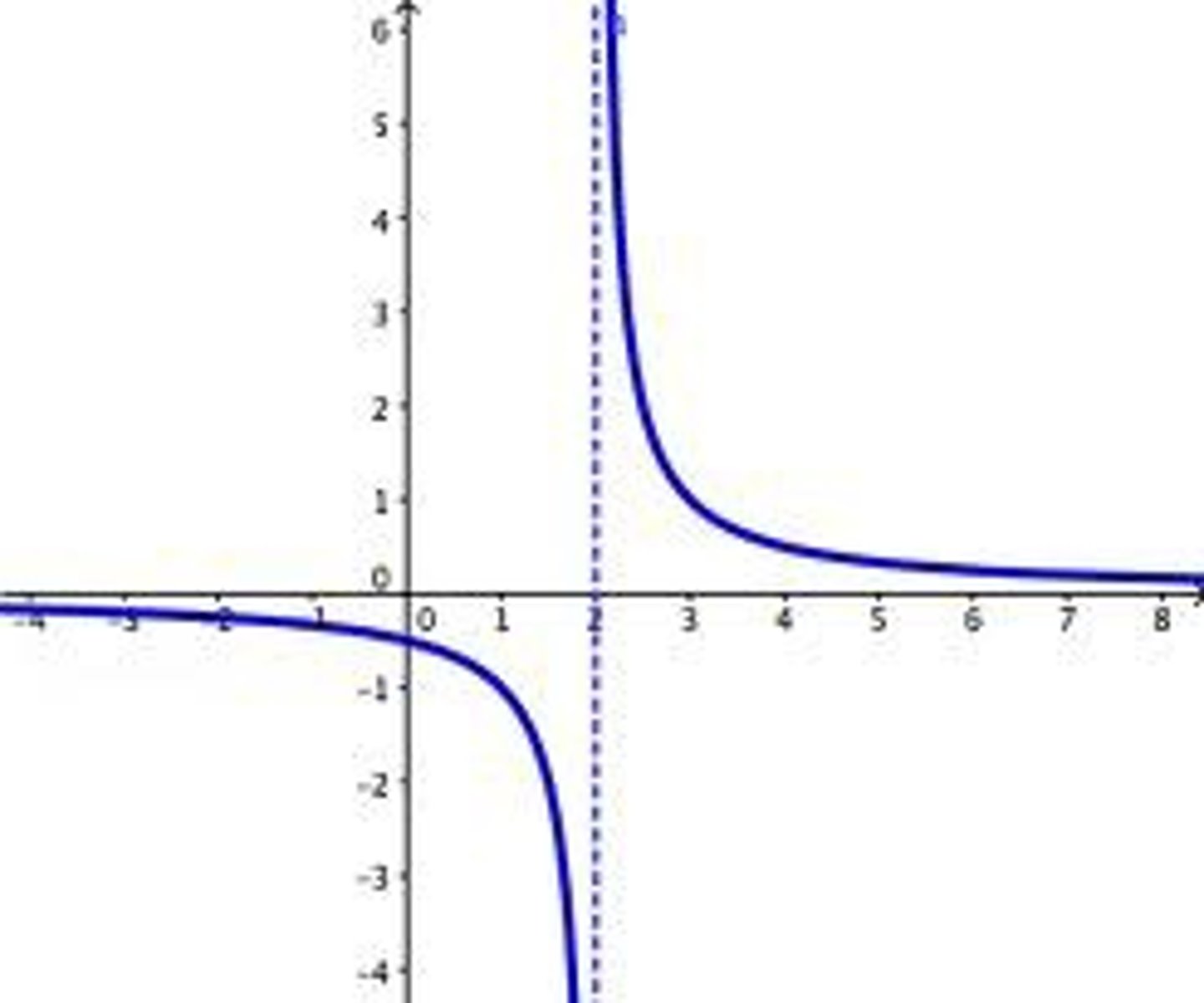
Vertical Asymptote

A vertical line that leaves the function undefined, not removable

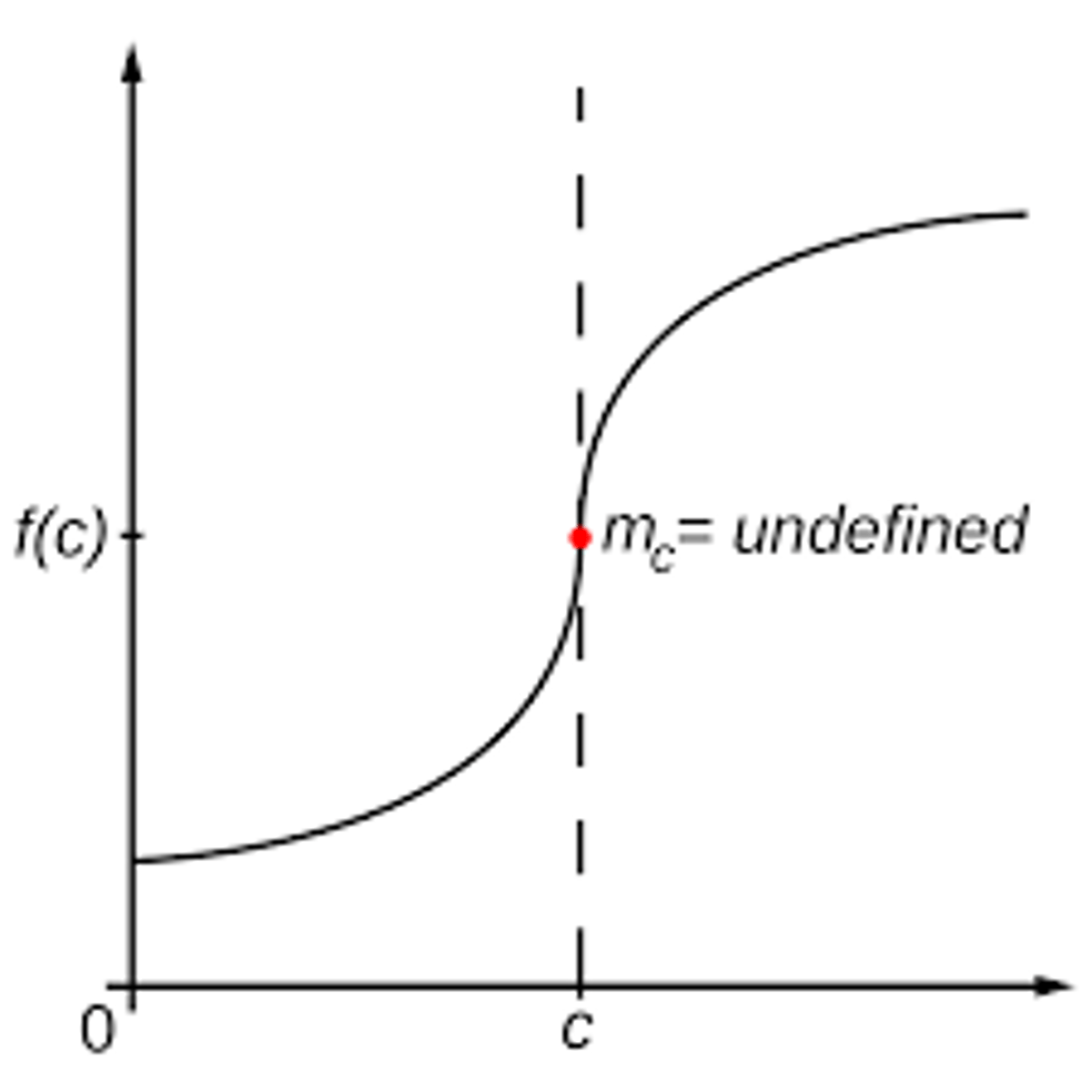
Vertical Tangent

a point where the slope of a curve is undefined

Horizontal Tangent

A point where the slope of the curve equals 0