Geometric Proofs

Segment Addition Postulate

If three points A, B, C are collinear and B is between A and C, then AB+BC=AC

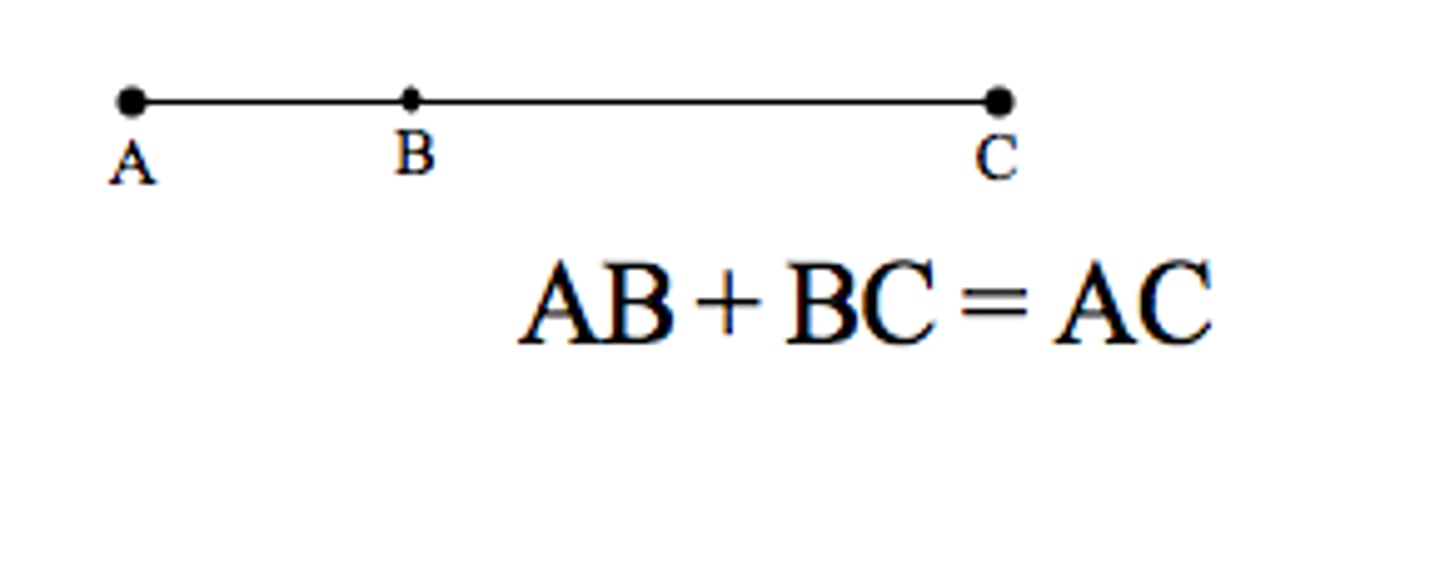
Definition of a Congruent

Segments or angles that have the same measure (Used when you switch from an "=" sign to a "≅" sign or vice versa)

Definition of a Bisector

a line or segment that intersects a segment or angle and divides it into two congruent halves

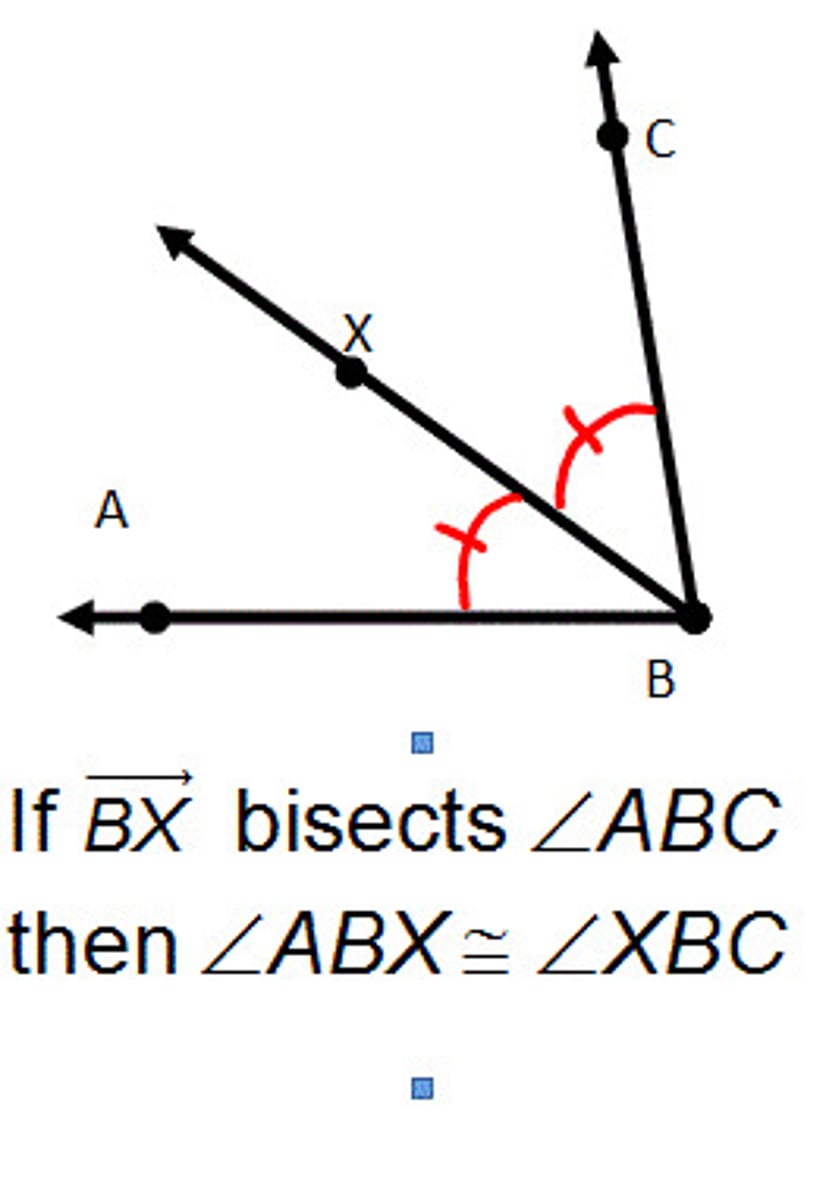
Definition of a Midpoint

divides the segment into two congruent segments

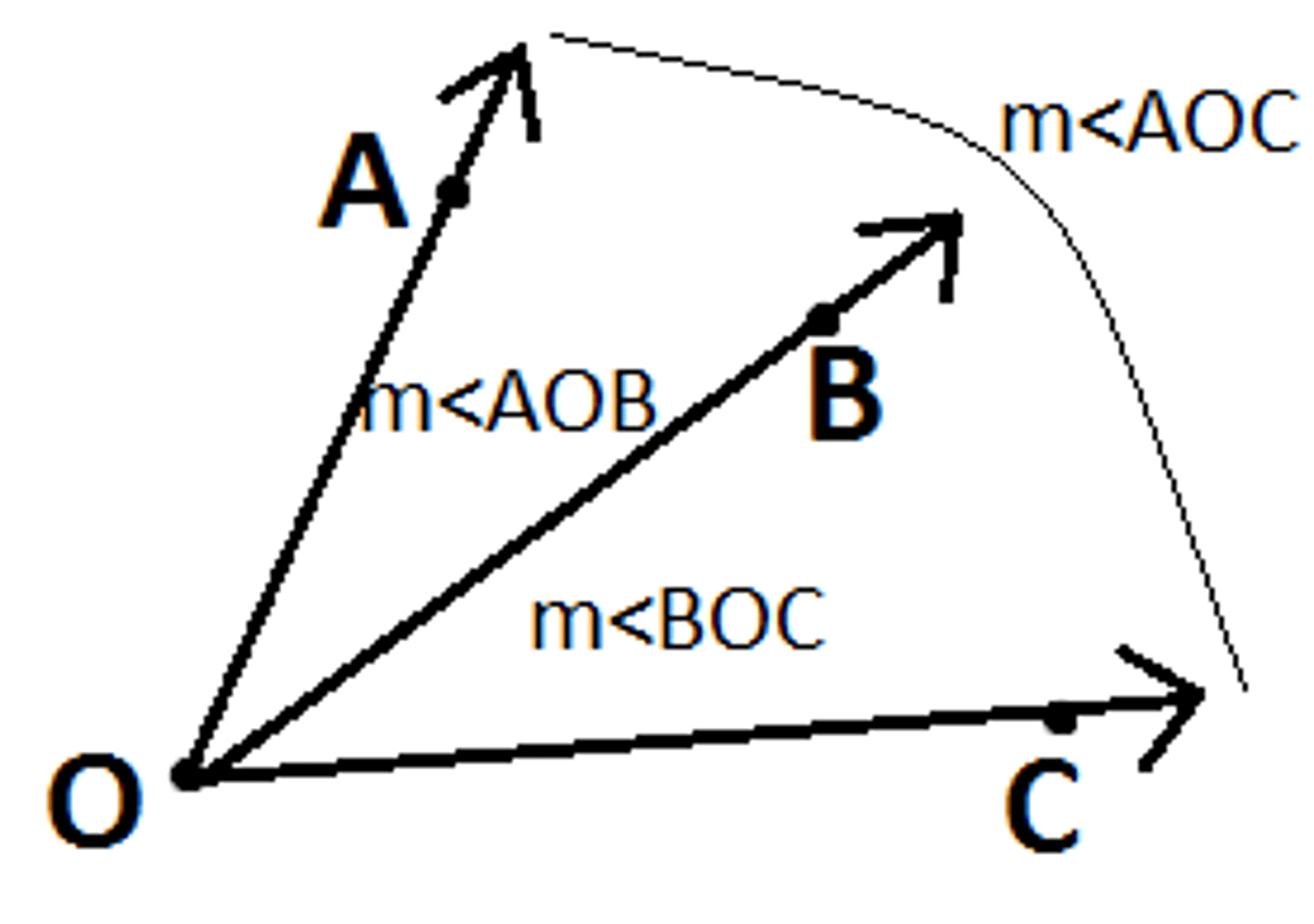
Angle Addition Postulate

If point B is in the interior of ∠AOC, then m∠AOB+m∠BOC=m∠AOC

Definition of Complementary Angles

two angles whose degree measures have a sum of 90º

Definition of Supplementary Angles

two angles whose degree measures have a sum of 180º

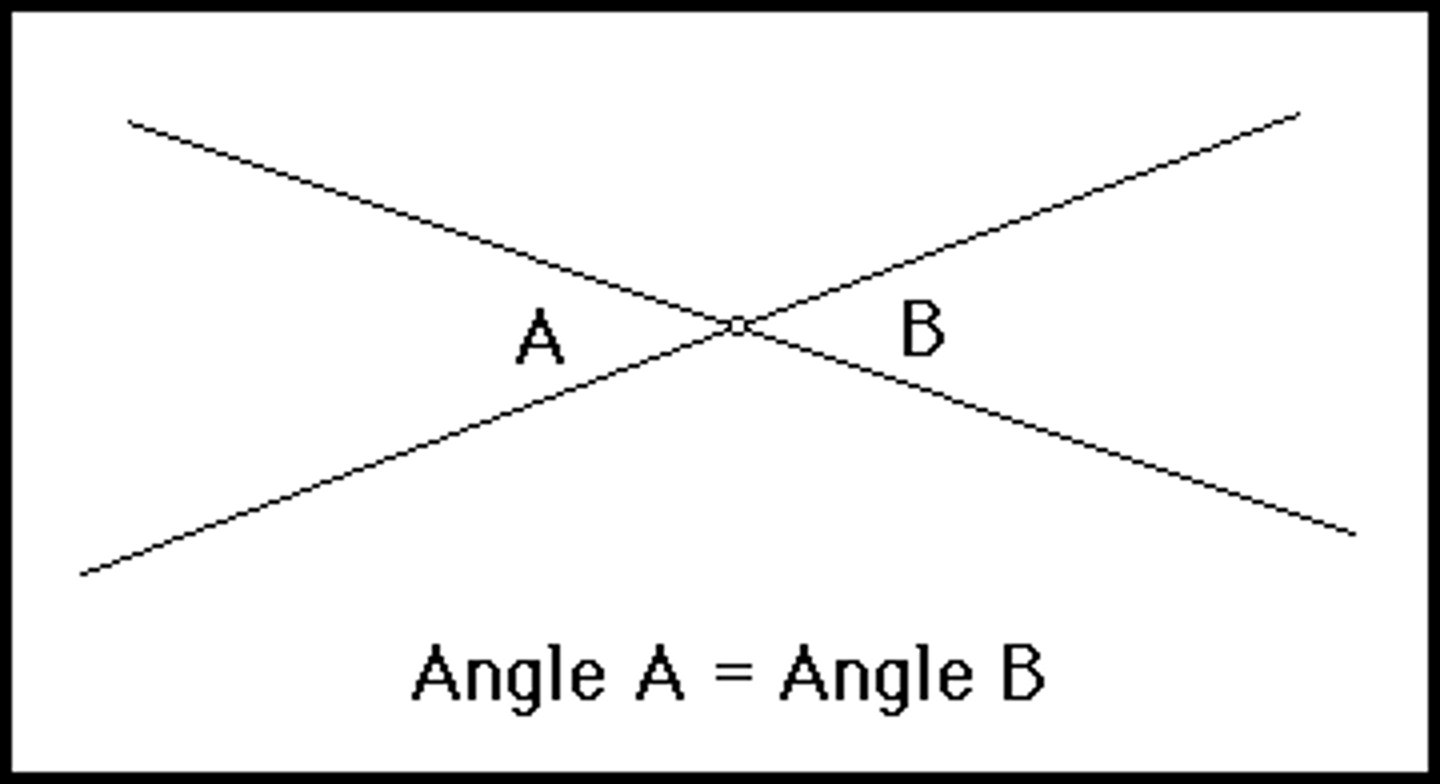
Vertical Angles Theorem

are always congruent and you can assume from a picture

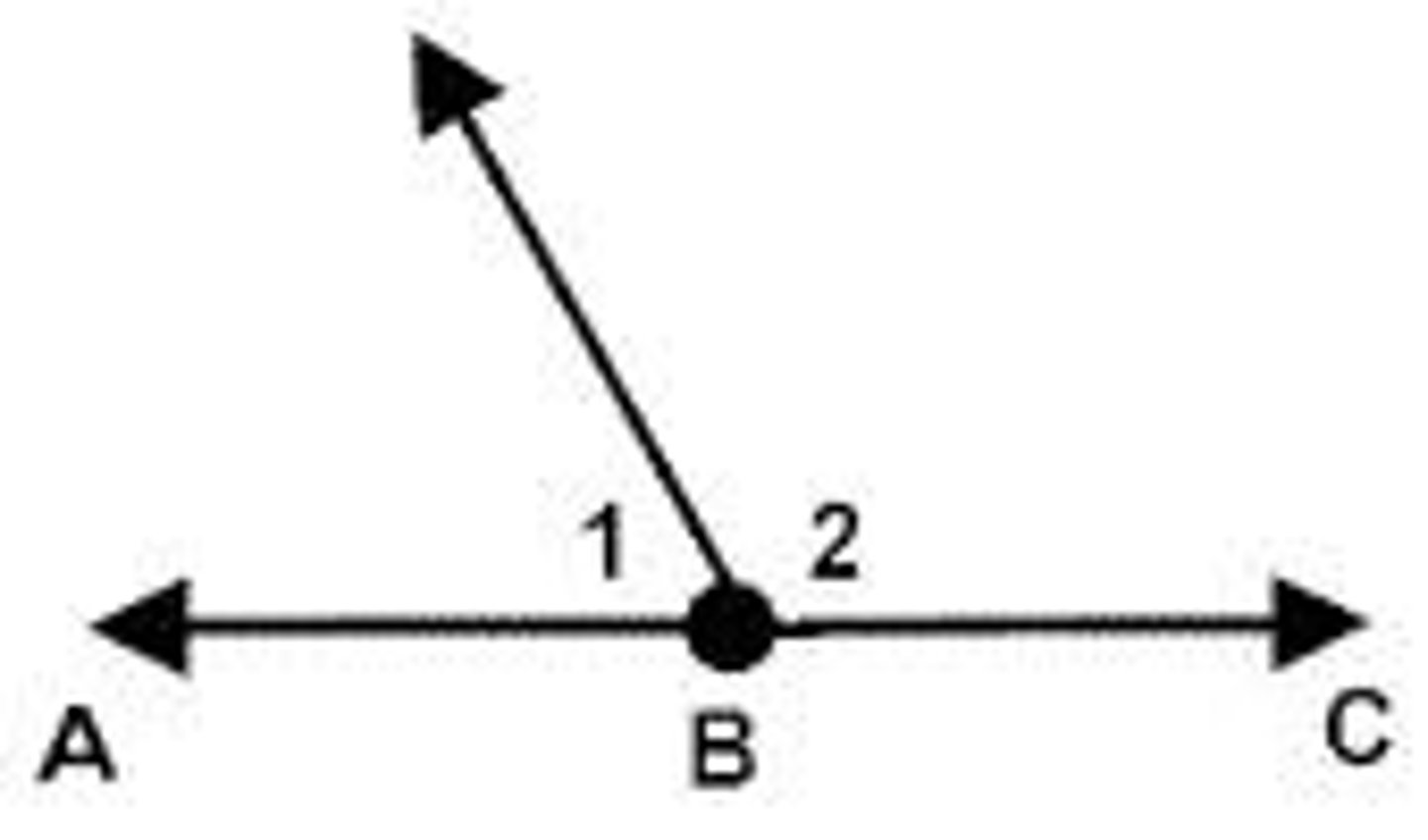
Linear Pair Theorem

you can assume from a picture; they are supplementary; Angle 1 + Angle 2 = 180

Reflexive Property of Equality

A line segment (or angle) is congruent to itself

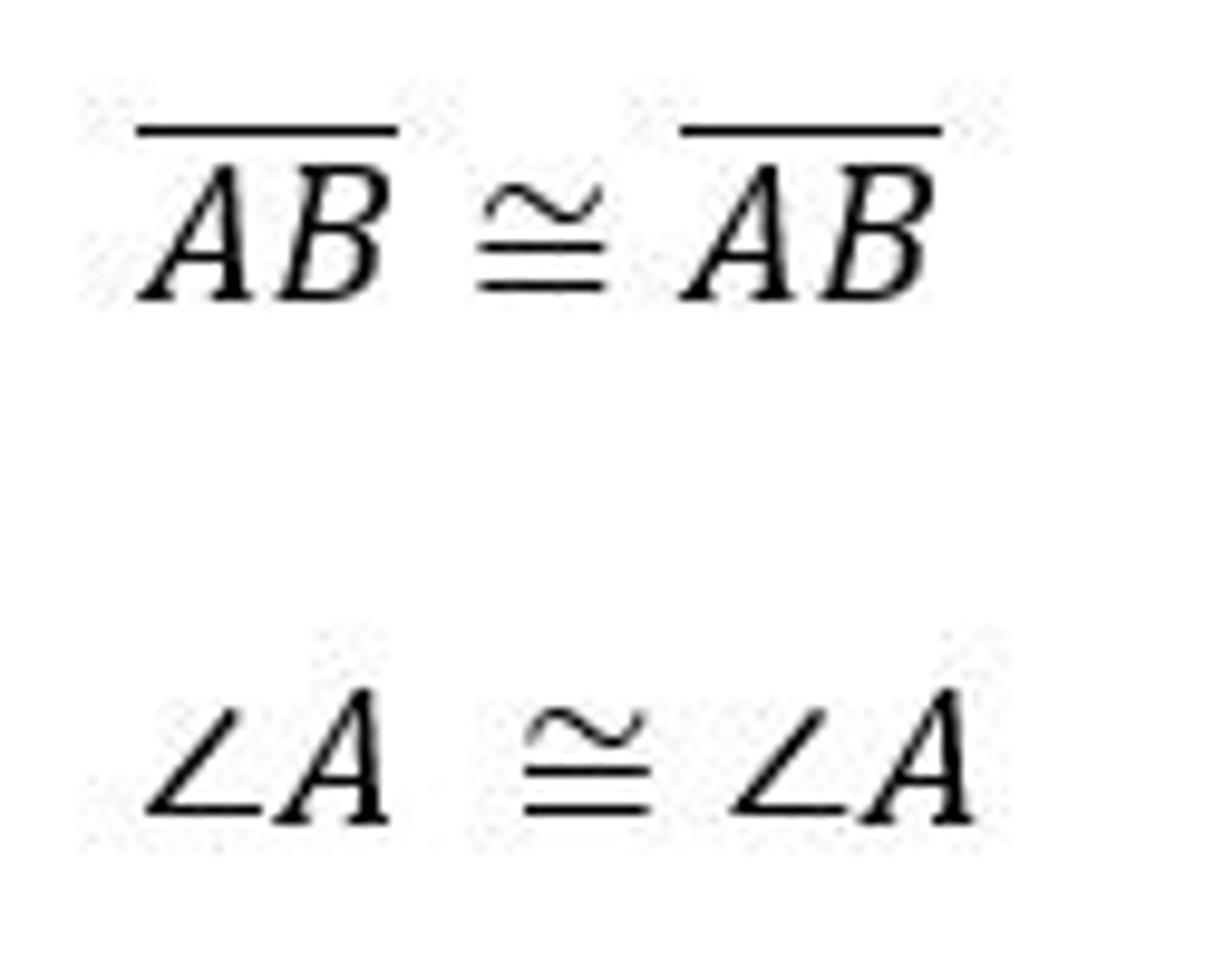
Symmetric Property of Equality

a=b, b=a; 8=x, x=8

Transitive Property of Equality

a=b, b=c, a=c [usually not = to a #]

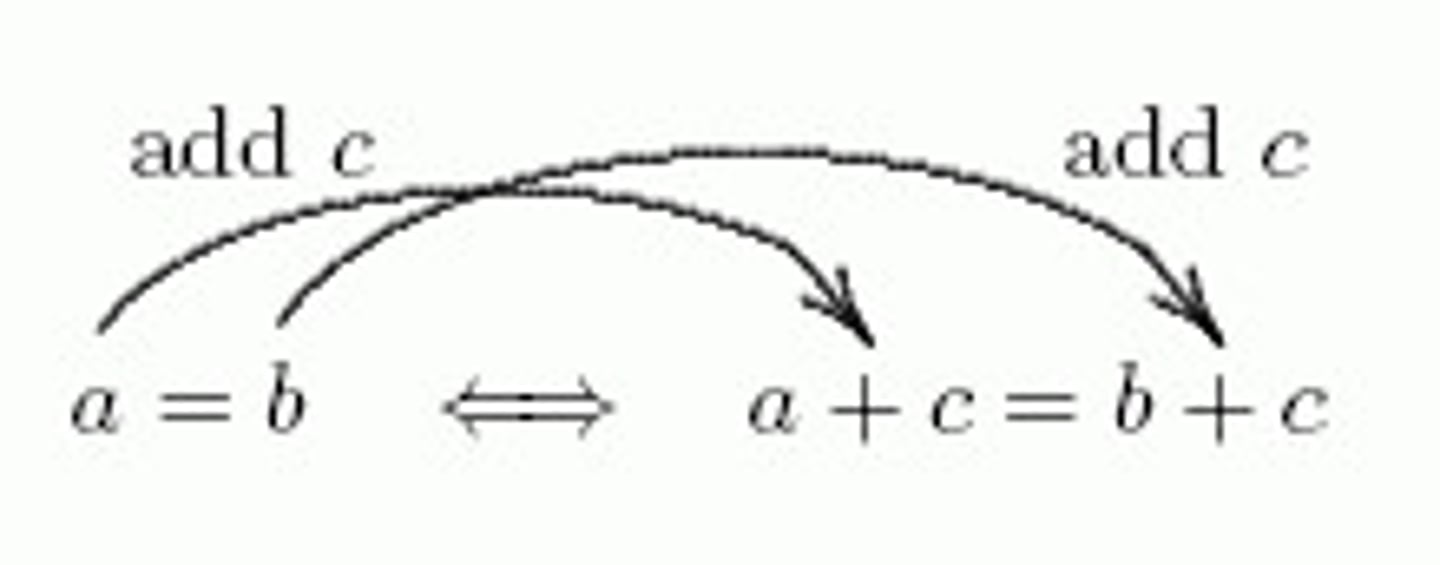
Addition Property of Equality

The same thing can be added to both sides of an equation

Subtraction Property of Equality

The same thing can be subtracted from both sides of an equation

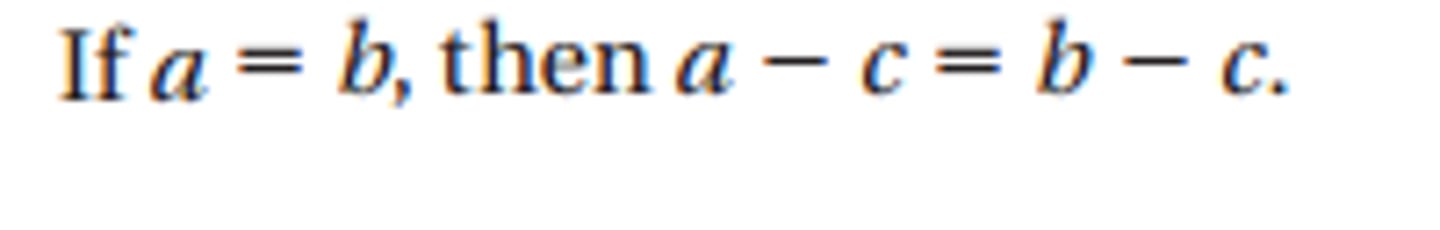
Multiplication Property of Equality

You can multiply both sides of an equation by the same thing

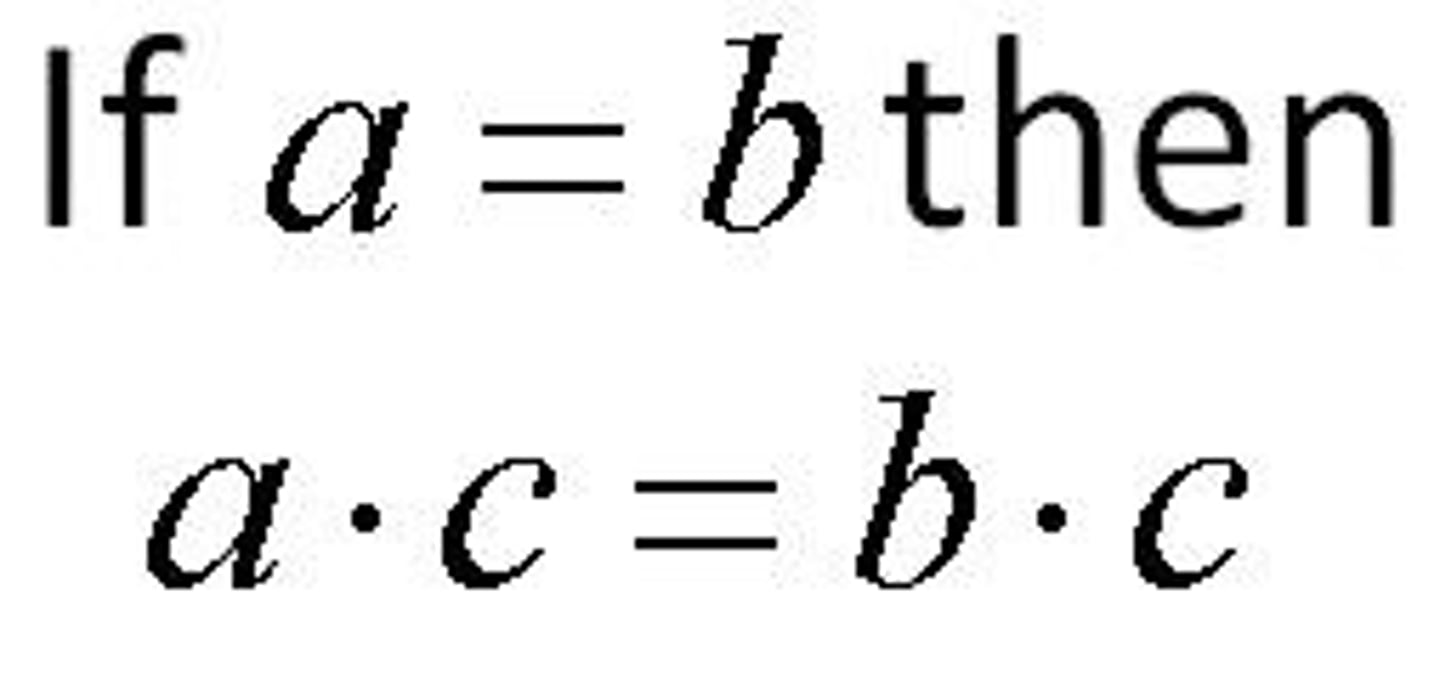
Division Property of Equality

You can multiply both sides of an equation by the same thing (except 0)

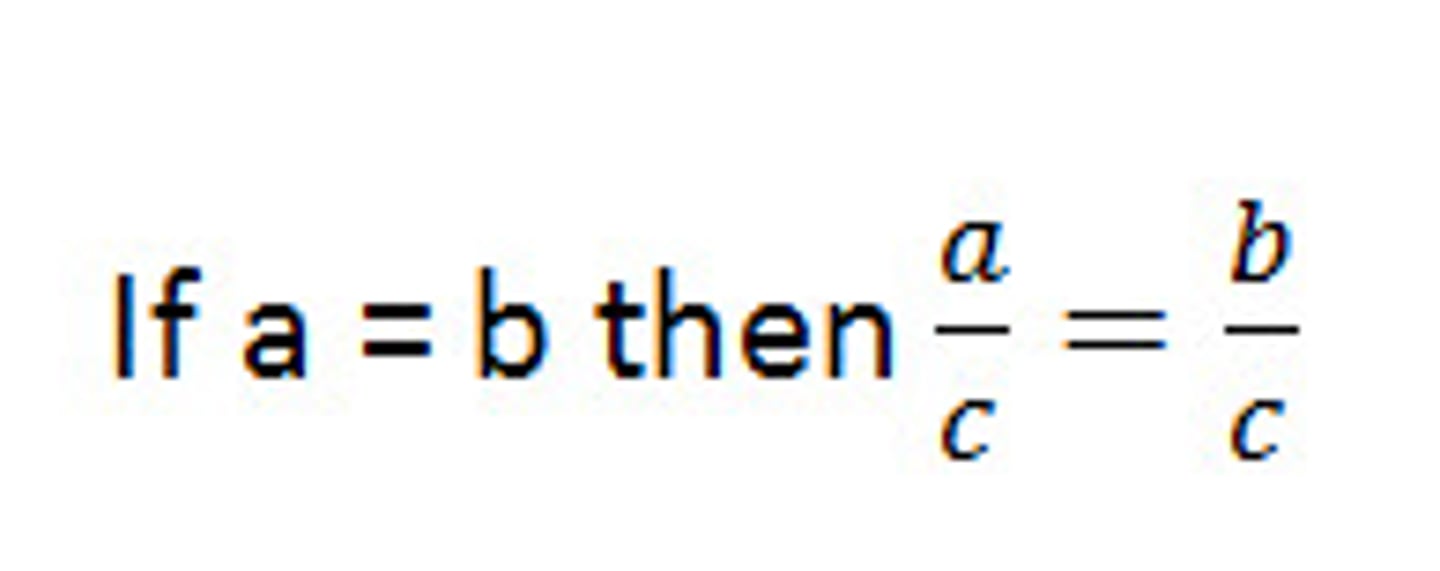
Substitution Property of Equality

Replace a variable or value with an equal variable or value

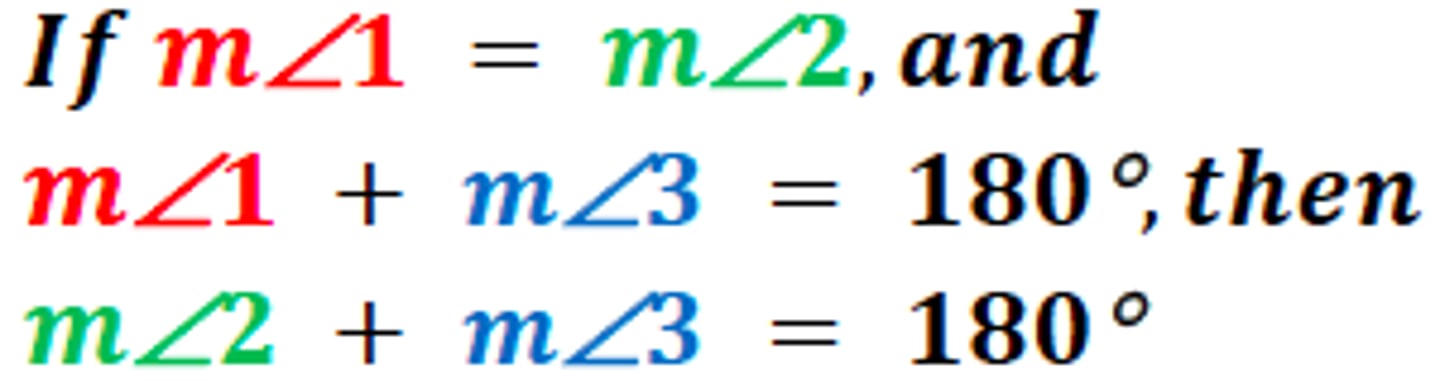
Distributive Property of Equality

a(b+c)=ab+ac

If Two Angles are Congruent and Supplementary

then each is a right angle

All Right Angles

are congruent to each other

Definition of Perpendicular Lines

Two intersecting lines that form four right angles

Definition of a Right Angle

measures 90º

Same Side Interior Angles Postulate

Angles inside two parallel lines on the same side of the transversal are supplementary

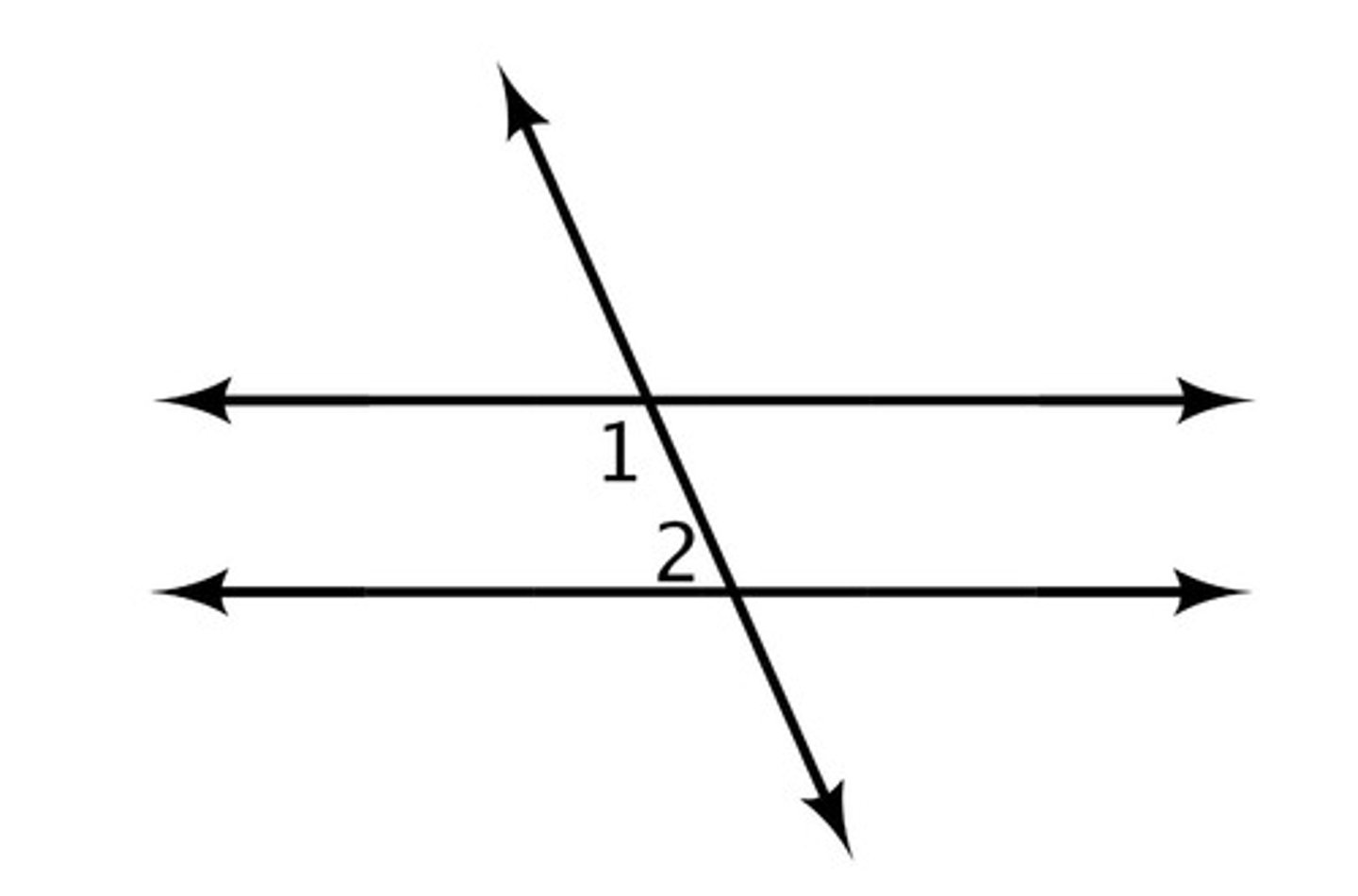
Alternate Interior Angles Theorem

Angles inside two parallel lines on opposite sides of the transversal are congruent

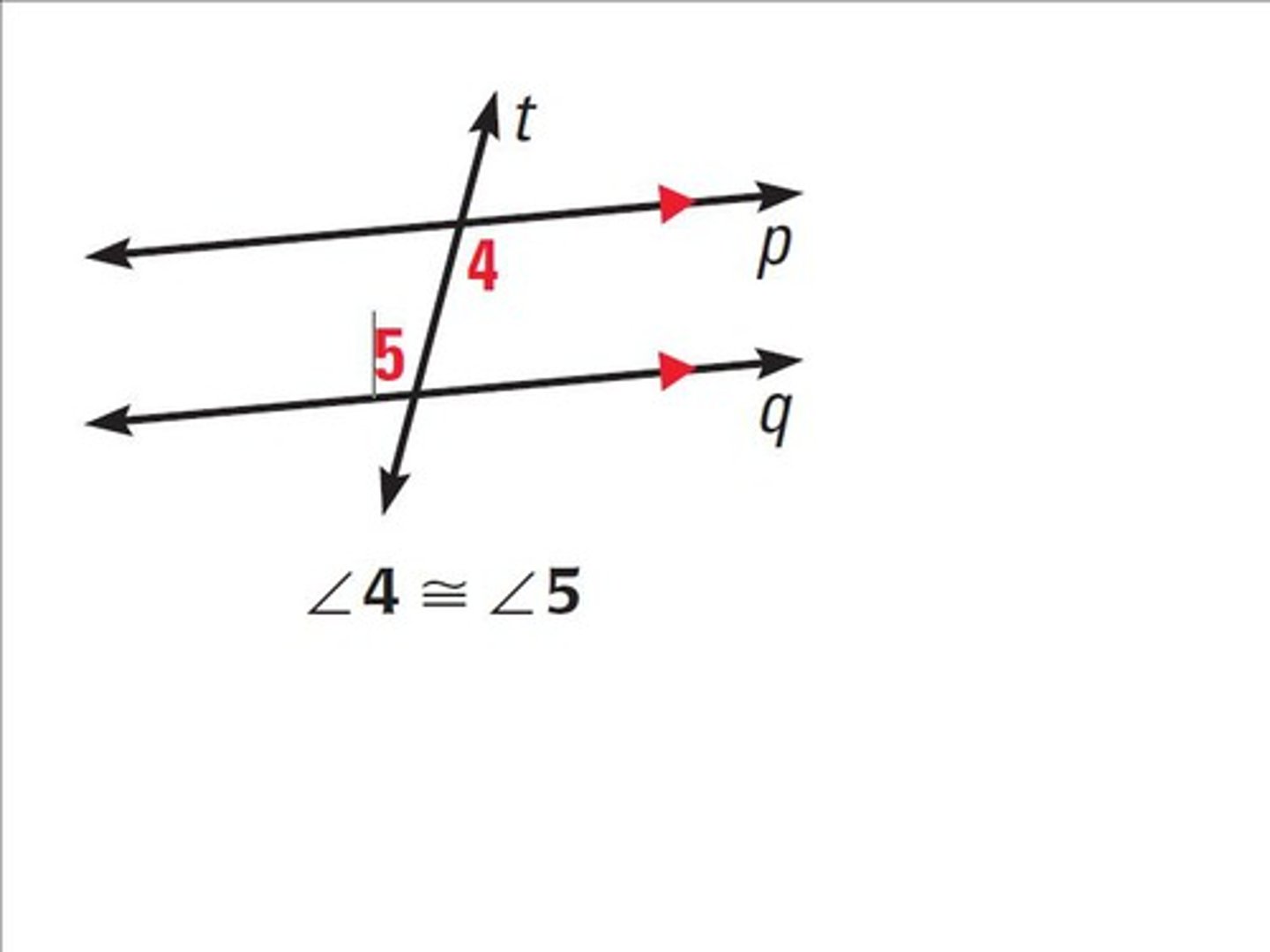
Corresponding Angles Theorem

The two angles are in the same position at each parallel line. They are congruent.

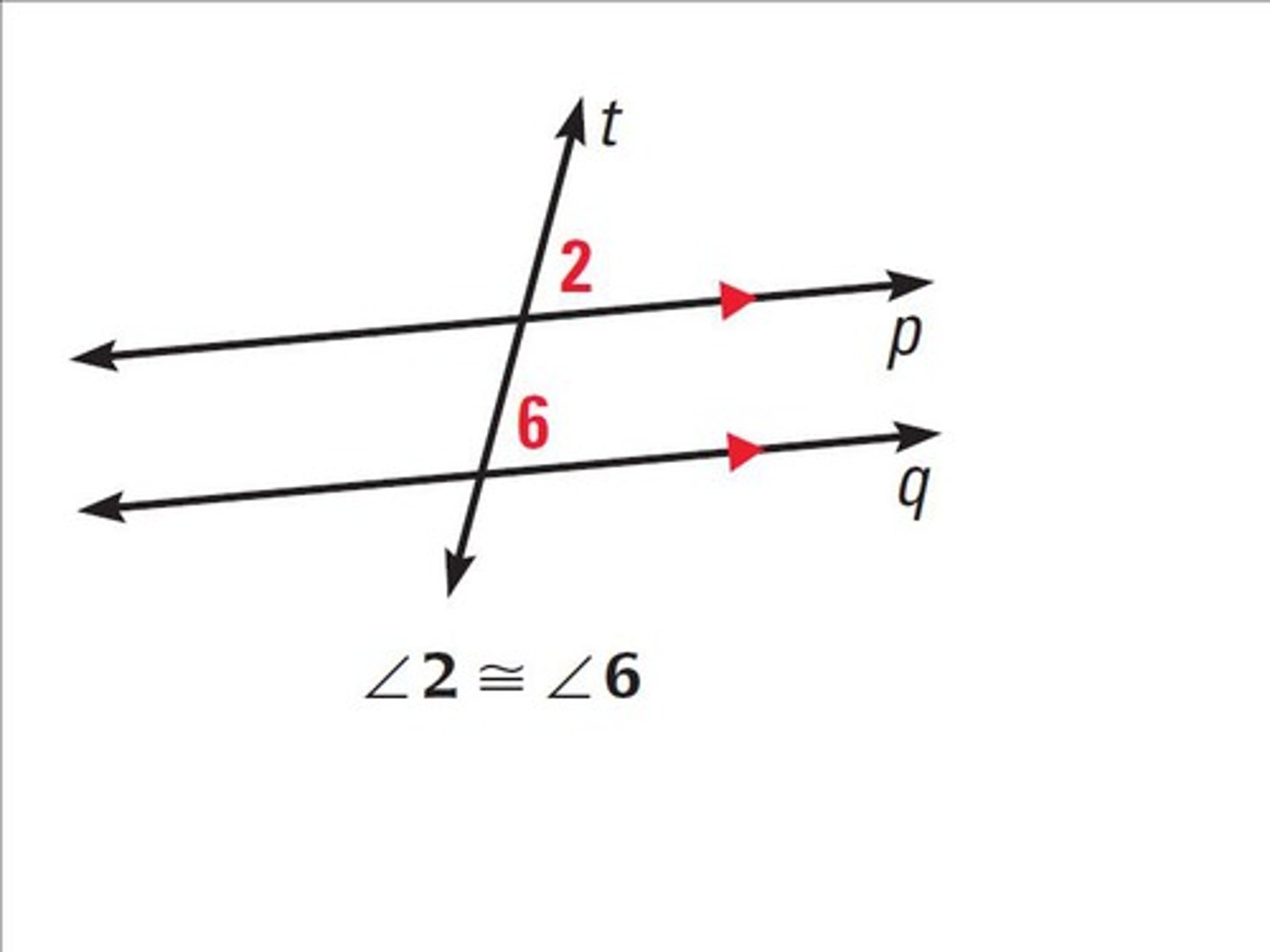
Alternate Exterior Angles Theorem

Angles outside two parallel lines on opposite sides of the transversal are congruent

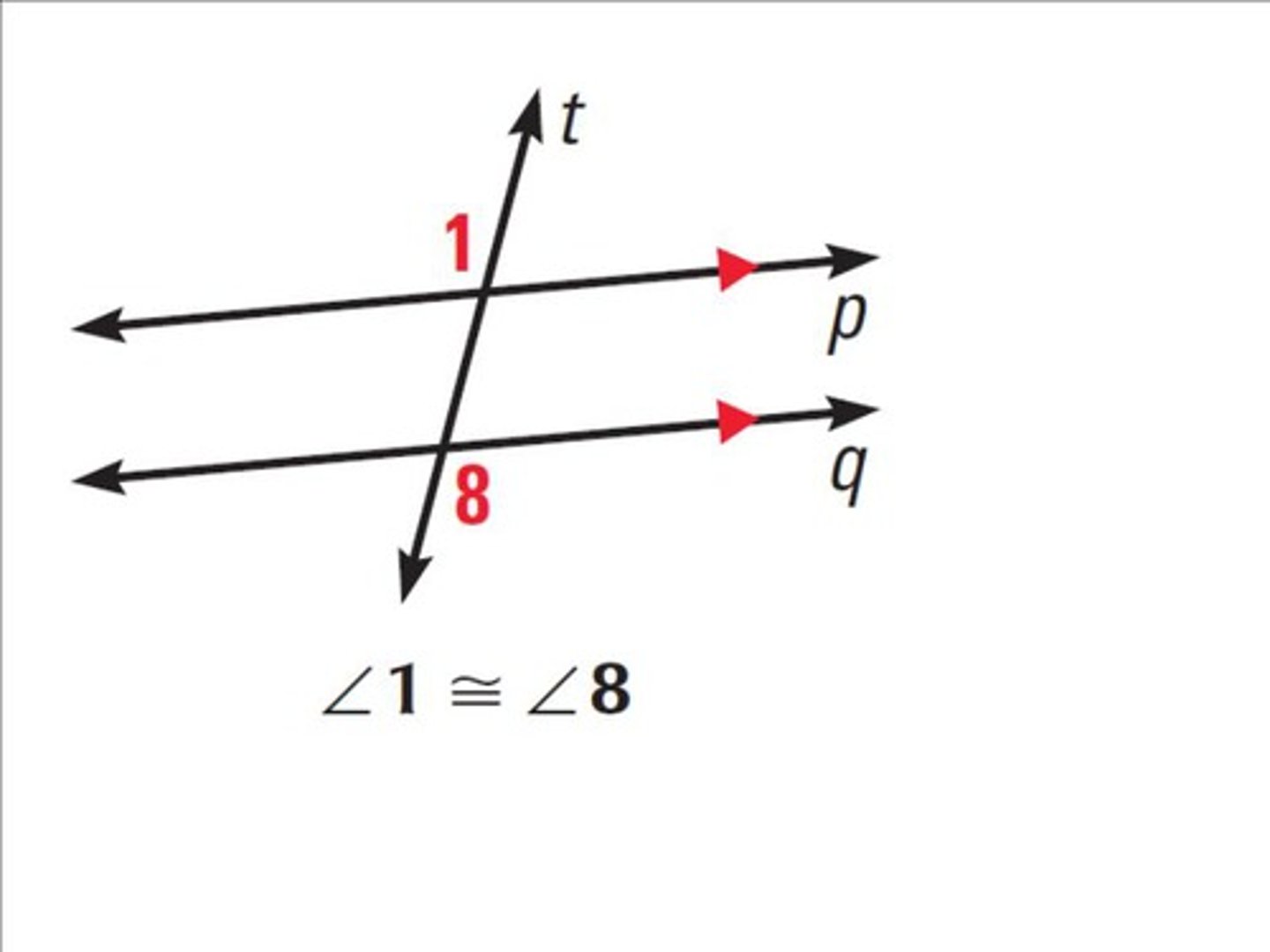
Converse of Same Side Interior Angles

if the converse of same side angles are supplementary, then the lines are parallel (used to prove lines are parallel)

Converse of Alternate Interior Angles Theorem

if the alternate interior angles are congruent, then the lines are parallel (used to prove lines are parallel)

Converse of Corresponding Angles Theorem

if the corresponding angles are congruent, then the lines are parallel (used to prove lines are parallel)

Converse of Alternate Exterior Angles Theorem

if the alternate exterior angles are congruent, then the lines are parallel (used to prove lines are parallel)

Two lines parallel to the same line

are parallel to each other